Для определения, какие прямые параллельны, если углы ∠QRP и ∠SPR равны, нужно проанализировать геометрическую фигуру на изображении.
На изображении дан прямоугольник ABCD, в котором отмечены точки P и Q на одной стороне прямоугольника, и точка R на другой стороне.
Первоначально, посмотрим на данную информацию и извлекаем следующие факты:
1. У нас есть две стороны прямоугольника, AB и BC, которые пересекаются в точке B.
2. Отмечены две точки P и Q на одной из сторон прямоугольника, AB.
3. Точка R отмечена на другой стороне прямоугольника, BC.
Теперь посмотрим на углы ∠QRP и ∠SPR. Мы можем заметить, что эти два угла находятся на прямых линиях, которые проходят через точки P и R.
Так как углы ∠QRP и ∠SPR равны, это означает, что эти два угла являются вертикальными углами. Вертикальные углы равны между собой.
Теперь мы проверяем, какие прямые параллельны. Из факта 2, мы знаем, что точки P и Q находятся на стороне AB. То есть, прямые AP и BQ параллельны, так как они являются сторонами прямоугольника и никогда не пересекаются.
Аналогично, точка R находится на стороне BC, поэтому прямые CR и BA также параллельны, так как они являются сторонами прямоугольника и никогда не пересекаются.
Итак, мы можем сделать вывод, что прямые AP и BQ параллельны, а также прямые CR и BA также параллельны, так как углы ∠QRP и ∠SPR равны.
Раз речь идёт об отрезках на осях координат, то уравнение плоскости надо рассматривать в форме, называемой "в отрезках".
Такое уравнение имеет вид: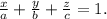
Здесь a, b c - отрезки на осях Ох, Оу и Оz, отсекаемые плоскостью.
Примем равные а и в за "к".
Получим уравнение плоскости (x/k) + (y/k) + (z/c) = 1.
Приведём к общему знаменателю.
cx + cy + kz = kc и подставим координаты заданных точек.
c3 + c5 + k1 = kc 8c +k = kc, (1)
c7 + c7 + k8 = kc 14c + 8k = kc. (2)
Вычтем из второго уравнения первое.
6c + 7k = 0 c = -7k/6. Подставим это значение в (1).
(-56k/6) + k = -7k²/6 -50k/6 = -7k²/6 k = 50/7, c = -50/6.
Получаем уравнение заданной плоскости:
(x/(50/7)) + (y/(50/7)) - (z/(50/6)) = 1 "в отрезках"
7x + 7y - 6z - 50 = 0 общее.