1. Прямая пересекает две стороны треугольника. Лежит ли она в плоскости этого треугольника?
Да.
По аксиоме: если две точки прямой лежат в плоскости, то вся прямая лежит в плоскости.
2. Прямая пересекает вершину треугольника. Лежит ли она в плоскости этого треугольника?
Необязательно.
У прямой и плоскости только одна общая точка, значит прямая может лежать в плоскости, а может ее пересекать.
3. Три вершины параллелограмма лежат в плоскости. Принадлежит ли четвертая вершина параллелограмма этой плоскости?
Да.
Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость. Значит плоскость параллелограмма совпадает с данной.
4. Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости?
Нет.
Плоскость окружности может пересекать данную плоскость по хорде.
5. Две пересекающиеся хорды окружности принадлежат плоскости. Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?
Да.
Через любые две пересекающиеся прямые проходит единственная плоскость. Значит плоскость, в которой лежит окружность, и данная плоскость совпадают.
6. Сколько плоскостей можно провести через: три различные точки;
если точки не лежат на одной прямой - одну;если точки лежат на одной прямой - бесконечно много;две различные точки;
бесконечно много;через прямую и не лежащую на ней точку;
одну;через две параллельные прямые?
одну.7. Верно ли утверждение: любые три точки принадлежат плоскости;
верно;через любые три точки проходит единственная плоскость?
неверно, надо уточнить: не лежащие на одной прямой.8. Известно, что прямая параллельна плоскости. Параллельна ли она любой прямой, лежащей в этой плоскости?
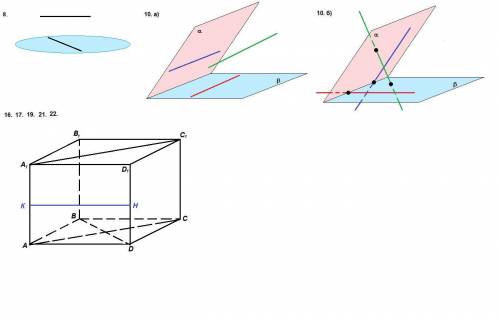
нет, прямая в плоскости и данная прямая могут быть скрещивающимися (см. рисунок);Может ли данная прямая пересечь какую-либо прямую, лежащую в плоскости?
нет, так как она не имеет с плоскостью общих точек.9. Средняя линия трапеции лежит в плоскости а. Пересекают ли основания трапеции эту плоскость?
Нет, они параллельны плоскости.
Основания и средняя линия параллельны, а если прямая параллельна прямой, лежащей в плоскости, то она параллельна плоскости.
10. а) Прямая а параллельна линии пересечения плоскостей α и β. Каково взаимное расположение а и α; а и β ?
а║α или а лежит в α; а║β или а лежит в β (на рисунке возможные расположения прямой а).10. б) Прямая b не параллельна линии пересечения плоскостей α и β Каково взаимное расположение b и α; b и β?
Прямая b может лежать в одной из плоскостей и пересекать другую или b может пересекать обе плоскости (см. рисунок).11. Сколько можно провести через данную точку: прямых, параллельных данной плоскости; плоскостей, параллельных данной прямой?
бесконечно много;12. Стороны АВ и ВС параллелограмма ABCD пересекают некоторую плоскость. Докажите, что прямые AD и DC пересекают эту плоскость.
Противоположные стороны параллелограмма параллельны, а если одна из параллельных прямых пересекает плоскость, то и другая пересекает эту плоскость.
13. Плоскость α параллельна одной из двух параллельных прямых. Каково взаимное расположение второй прямой и плоскости α?
Вторая прямая может лежать в плоскости, а может быть ей параллельна.
14. Сторона АВ параллелограмма ABCD лежит в плоскости α. Докажите, что сторона CD параллельна этой плоскости.
CD║AB как противоположные стороны параллелограмма, АВ лежит в плоскости, значит CD параллельна плоскости (признак параллельности прямой и плоскости)
15. Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой?
Нет, параллельные прямые должны лежать в одной плоскости.
16. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны?
Нет, они могут быть скрещивающимися или пересекающимися
на рисунке для плоскости (АВС) КН и D₁C₁ скрещивающиеся, А₁С₁ и А₁В₁ пересекающиеся.
17. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость?
Эти прямые могут быть скрещивающимися или пересекающимися.
На рисунке для плоскости (АВС) А₁В₁ и СС₁ скрещивающиеся, а А₁В₁ и ВВ₁ пересекающиеся.
19. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными? Пересекаться?
Да.
На рисунке АА║ВВ₁, они скрещиваются с прямой DC; а прямые АА₁ и КН пересекаются, но тоже скрещиваются с прямой DC.
20. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой?
Нет, если две прямые параллельны третьей, то они параллельны между собой, а данные прямые скрещивающиеся.
21. Прямая, не лежащая в плоскости параллелограмма, параллельна одной из его диагоналей. Каково взаимное расположение данной прямой и второй диагонали?
Скрещивающиеся.
На рисунке А₁С₁║АС, но А₁С₁ и BD скрещивающиеся.
22. Как могут быть расположены прямая и плоскость, если данная прямая и некоторая прямая, лежащая в этой плоскости, скрещиваются?
Прямая может быть параллельна плоскости, а может ее пересекать.
На рисунке для плоскости (АВС) А₁С₁ и BD скрещивающиеся, А₁С₁║(АВС); АА₁ и BD скрещивающиеся, АА₁∩(АВС).
дано: ab=ad,
∠bac=∠dac
доказать: ∆abc=∆adc
доказательство:
1) ab=ad (по условию)
2) ∠bac=∠dac (по условию)
3) ac — общая сторона.
следовательно, ∆abc=∆adc (по двум сторонам и углу между ними)
дано:
ao=bo,
co=do
доказать: ∆aoc=∆bod.
доказательство:
определяем те элементы, о равенстве которых известно по условию :
1) ao=bo (по условию)
2) co=do (по условию).
3) ∠aoc = ∠bod (как вертикальные).
дано:
ab=ac,
af=ak
доказать: ∆abk=∆acf
доказательство:
1) ab=ac (по условию)
2) af=ak (по условию)
3) ∠a — общий.
следовательно, ∆abk=∆acf (по двум сторонам и углу между ними).
вычислите периметр равнобедренного треугольника авс, если периметр треугольника adc равен 18 cм, и cd = 6 cм и ad = bd (fig.5)
доказательство:
периметр треугольника adc = ac + cd + ad = 18 ⇔ ac + 6 + ad = 18 ⇔ ac + ad = 12
потому что ac = bc (треугольники являются равнобедренными) и ad = db, следовательно ac + ad = db +bc = 12
периметр треугольника abc = ab + ac + bc = ad + db + ac + bc = 12 + 12 = 24 cм.