1. Координатная плоскость состоит из: двух взаимно – перпендикулярных осей
2. Координатная система делит плоскость в) на 4 четверти.
3. Начало координат имеет координаты:а) (0;0);
4. Точка, лежащая в I четверти, имеет координаты: а) (x; y);если х и у - положительные числа
5. Точка, лежащая в II четверти, имеет координаты: в) (-x; y). если х и у положительные числа
6. Точка, лежащая в III четверти, имеет координаты:б) (-x;-y);если х и у положительные числа
7. Точка, лежащая в I V четверти, имеет координаты:в) (x;-y).если х и у положительные числа
8. Точка, лежащая на OX , имеет координаты: а) (-x;0);
б) (x;0);
9. Точка, лежащая на Oy , имеет координаты:а) (0;y);
б) (0;-y);
10. Угол в каждой четверти равен:в) 90⁰.
1. По одному из теорем сторон ∆, мы узнаем, что AD=AB-BD=19-9,5=9,5см
DC=BC-BD=19-9,5=9,5см
2. По правилу: катет лежащий напротив угла в 30° равен половине гипотенузы
Находим, что если АD=1/2AB, то угол ABD=30°. То же самое и с ∆BCD.
3. Из правила: сумма острых углов прямоугольного треугольника равна 90°
Находим, что угол ВАС= углу ВСА= 60°
4. Теперь найдем общий угол АВС= АВD+CBD=30+30=60°
5. Это уже дополнительно, но из всего этого можно добавить, что ∆АВС не только равнобедренный, но и равносторонний
6. Также хочу уточнить, что высота ВD разделила ∆АВС на прямоугольные треугольники ∆ ABD и ∆BCD, в которых угол D равен 90°
ОТМЕТЬ, КАК ЛУЧШИЙ ОТВЕТ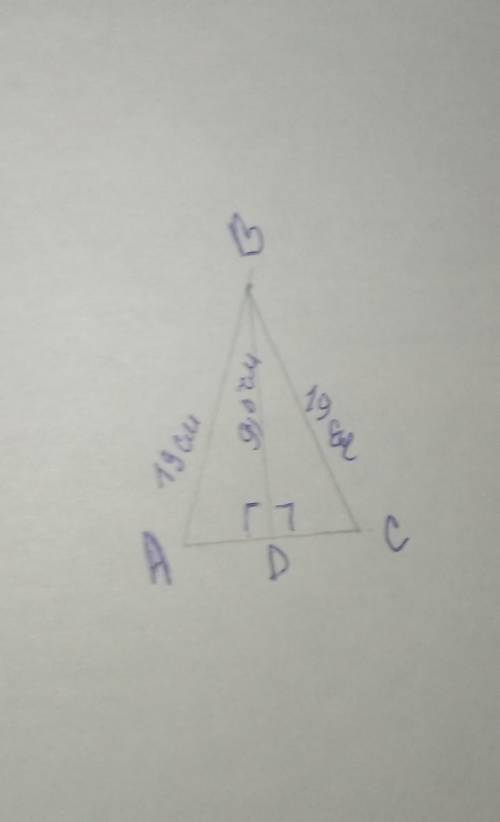
Пусть дана равнобедренная трапеция АВСD. Из условия ясно, что точка М проецируется в центр О вписанной в трапецию окружности, так как расстояние от точки М до стороны - это перпендикуляр из точки М к стороне, а радиус вписанной окружности - перпендикуляр из точки О на плоскости трапеции к ее стороне. Основания этих перпендикуляров находятся в одной точке по теореме о трех перпендикулярах. Диаметр вписанной в нашу трапецию окружности пройдет через середины ее оснований, значит боковая сторона трапеции будет равна сумме двух отрезков: половин большего и меньшего оснований, так как касательные из одной точки к окружности равны, то АР=АН и ВР=ВN (см. рисунок). Но ОР - это высота из прямого угла треугольника АОВ (боковая сторона видна под углом 90° из центра вписанной окружности - свойство). и по ее свойству равна ОР = √(АР*ВР) = √(2*4,5) = 3 ед. Тогда по Пифагору из прямоугольного треугольника МОР найдем искомое расстояние МО.
МО=√(МР²-ОР²) = √(5²-3²) = 4 ед. Это ответ.