Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.
Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.
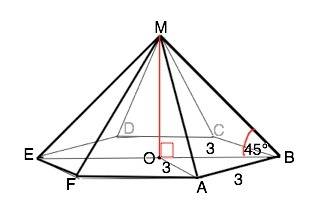
Обозначим пирамиду ABCDEF, центр - О.
Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.
Объём пирамиды равен 1/3 произведения высоты на площадь основания.
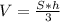
Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:
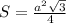
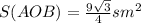
Площадь основания
6•9√3/4 sm²
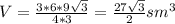
Р=3R*sqrt(3)
Откуда
R=P/3*sqrt(3)=45/3*sqrt(3)=15*sqrt(3)
Радиус окружности описанной около восьмиугольника определяется по формуле
R=a/2sin(360/16)=a/2sin(22,5°)
Откуда
a=R*2sin(22,5°)=2*15*sqrt(3)*sin(22,5°)=30*1,7*0,38=19,38
2. Площадь квадрата равна
S=a^2
Определим радиус окружности
R^2=a^2+a^2=2a^2
Площадь круга равна
Sк=pi*R^2=2*pi*a^2=144*pi
3. L=pi*r*a/180, где a – градусная мера дуги, r- радиус окружности
L=pi*3*150/180=2,5*pi
4. Сторона квадрата равна p/4=48/4=12
Диагональ квадрата равна
d^2=a^2+a^2=144+144=288
d=12*sqrt(2)
Радиус квадрата вписанного в окружность равна
R=d/2=6*sqrt(2)
Сторона правильного пятиугольника L, вписанная в эту окружность равна
L=2R*sin(36°)=12*sqrt(2)*sin(36°)=12*1,4*0,588=9,88
5. Площадь кольца находим по формуле:
S=pi* (R^2−r^)
S=pi*(7^2-3^2)=pi*(49-9)=40*pi
6. Треугольник равносторонний, так как угол равен 60°, радиус окружности равен 4
Найдем площадь треугольника по формуле
Sт=R^2*sqrt(3)/4
Sт=16*sqrt(3)/4=4*sqrt(3)
Найдем площадь сектора по формуле
Sc=pi*R^2*(60/360)=pi*16/6==8*pi/3
Найдем площадь сегмента
Sсм=Sс-Sт=8*pi/3-4*sqrt(3)=1,449
Если в четырёхугольник можно вписать окружность, значит у него суммы противоположных сторон равны.
В равнобедренной трапеции боковые стороны равны. Сумма боковых сторон 12+12=24 см, значит сумма оснований тоже 24.
периметр трапеции равен 48 см