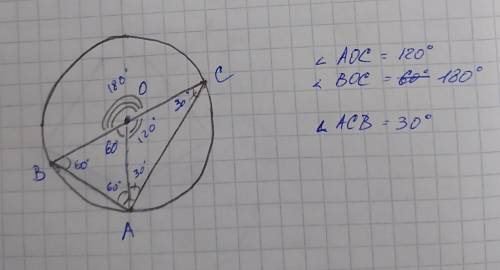
2. ∠AOC = 120°; ∠BOC = 180°; ∠ACB = 30°
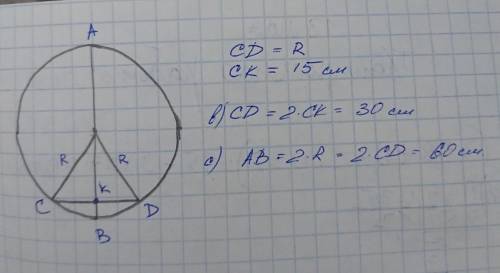
3. CD = 30 см; AB = 60 см
Объяснение:
2. Упростим соотношение дуг: 3:9:6 <=> 1:3:2 <=> AB, BC, AC
Найдём их градусную меру:
AB + BC + AC = x + 3x + 2x = 360°
6x = 360°
x = 60°
AB - 60°
BC - 180°
AC - 120°
Отразим это на рисунке.
Легко видеть, что
∠AOC = 120°; ∠BOC = 180°
На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
3. Рисунок и решение на фото.
Объяснение:
Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей.
Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной.
Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма
Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.
Геометрические места точек.
Решение задач с геометрических преобразований и геометрических мест.
Теорема Чевы и теорема Менелая.
Эллипс, гипербола, парабола как геометрические места точек.
Неразрешимость классических задач на построение.
Треугольникомназывается фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинамитреугольника, а отрезки - его сторонами.
Биссектриса
Биссектриса угла – это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
· Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
· Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.
· Биссектрисы внутреннего и внешнего углов перпендикулярны.
· Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника.
· Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
Напомню, что расстояние от точки до прямой называется перпендикуляр, опущенный из данной точки на прямую.
Рассмотрим ΔASB - равносторонний ( по условию все ребра = 1), то опустим SH ⊥ AB. По свойству равностороннего треугольника: AH = HB = 0,5.
Рассмотрим ΔSHB - прямоугольный: SB = 1; HB = 0,5. Нужно найти катет SH, то по т.Пифагора: SH = √(SB^2 - HB^2) = √3/√4 = √3/2
ответ: √3/2