Объяснение: ЗАДАНИЕ 1
Сумма угло ромба и любого четырёхугольника составляет 360°. У ромба противоположные углы между собой равны, поэтому легко можно найти каждый угол:
360-226=134°
Нам известны попарно суммы углов, теперь найдём каждый из них:
226÷2=113°
134÷2=67°
ответ: острый угол ромба =67°
ЗАДАНИЕ 2
Найдём площадь пола:
Sпол=12,5×5,4=67,5м²
Переведём площадь в сантиметры:
67,5×100=6750см²
Теперь найдём площадь дощечки:
S=25×10=250см²
Теперь поделим эти площади друг на друга: 6750÷250=27дощ
ответ: 27дощ.
ЗАДАНИЕ 3
Найдём гипотенузу по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
Гипот=√(16²+30²)=√(256+900)=
=√1156=34см
Итак гипотенуза=34см
Так как медиана проведена к гипотенузе, то она проведена из прямого угла, поэтому медиана равна половине гипотенузы: 34÷2=17см
ответ: медиана=17см
ЗАДАНИЕ 4
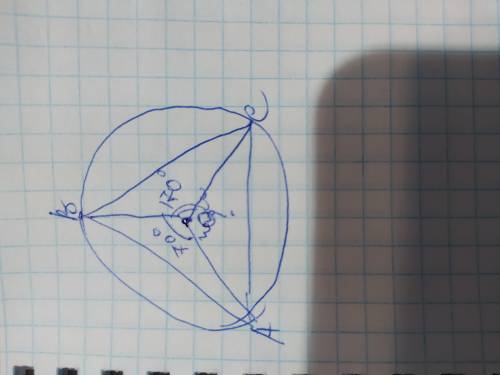
Сумма всех углов окружности составляет 360°, и так как нам известны 2 из них, найдём искомый:
Угол дуги АС=360-70-170=120°
ОТВЕТ: угол дуги АС=120°
Объяснение: ЗАДАНИЕ 1
Сумма угло ромба и любого четырёхугольника составляет 360°. У ромба противоположные углы между собой равны, поэтому легко можно найти каждый угол:
360-226=134°
Нам известны попарно суммы углов, теперь найдём каждый из них:
226÷2=113°
134÷2=67°
ответ: острый угол ромба =67°
ЗАДАНИЕ 2
Найдём площадь пола:
Sпол=12,5×5,4=67,5м²
Переведём площадь в сантиметры:
67,5×100=6750см²
Теперь найдём площадь дощечки:
S=25×10=250см²
Теперь поделим эти площади друг на друга: 6750÷250=27дощ
ответ: 27дощ.
ЗАДАНИЕ 3
Найдём гипотенузу по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
Гипот=√(16²+30²)=√(256+900)=
=√1156=34см
Итак гипотенуза=34см
Так как медиана проведена к гипотенузе, то она проведена из прямого угла, поэтому медиана равна половине гипотенузы: 34÷2=17см
ответ: медиана=17см
ЗАДАНИЕ 4
Сумма всех углов окружности составляет 360°, и так как нам известны 2 из них, найдём искомый:
Угол дуги АС=360-70-170=120°
ОТВЕТ: угол дуги АС=120°

Обозначим трапецию АВСD, высоту, опущенную из вершины С - СН.
. Площадь трапеции равна произведению высоты на полусумму оснований. Полусумма оснований=средняя линия трапеции.
Вспомним, что в равнобедренной трапеции высота, проведенная из тупого угла к основанию, делит его на отрезки. больший из которых равен полусумме оснований, меньший - их полуразности.⇒ АН=4. ⇒ S(ABCD)=CH•AH.Треугольник АСН - прямоугольный. По т.Пифагора СН=√(AC²-AH²)=√(6²-4²)=2√5 ⇒ S(ABCD)=2√5•4=8√5 (ед площади).
Или
Проведем из вершины С параллельно диагонали ВD прямую до пересечения с продолжением АD в точке К. Четырехугольник DBCK- параллелограмм (противолежащие стороны параллельны), DK=BC и АК=ВС+AD=2•4=8(т.к. равно двум полусуммам оснований). Тогда площадь треугольника равна АСК равна площади трапеции, её можно вычислить по ф.Герона и получить тот же результат.