Для начала необходимо привести уравнение окружности к стандартному виду: (x-a)²+(y-b)²=r² , где (a;b) - центр , r - радиус.
Для этого свернём выражение как 2 квадрата разности
Думаю, это нужно сделать детально.
x²-10x=(x-5)²-25
y²-2y=(y-1)²-1
20=20
Если сложить все 3 уравнения, то получится:
x²+y²-10x-2y+20=(x-5)²-25+(y-1)²-1+20. Так как начальное выражение(слева) было равно 0, то и правая часть тоже. Имеем:
(x-5)²-25+(y-1)²-1+20=0
(x-5)²+(y-1)²=6 Отсюда видим, что центр окружности (5;1) , а радиус √6
2)Значит нам нужна прямая, параллельная y=7x-2.
Прямые параллельны, если у них одинаковый угловой коэффициент(цифра перед х)
Запишем уравнение прямой в общем виде
y=kx+m. Мы знаем угловой коэффициент и точку, принадлежащую прямой(центр окружности). Подставим всё
1=7*5+m ⇔ m= -34
Итого имеем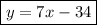 
- уравнение нашей прямой
1)
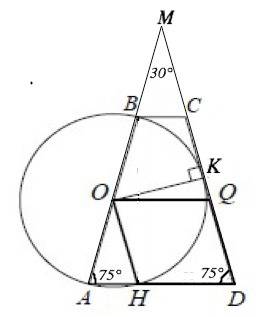
О- центр окружности ⇒ середина АВ, Q - середина СD.
ОQ соединяет середины боковых сторон трапеции ⇒
OQ как средняя линия трапеции параллельна АD.
Т.к. трапеция равнобедренная, АО=DQ
Углы при основании равнобедренной трапеции равны, АО=НО ( радиусы), треугольник АОН - равнобедренный,∠ОНА=∠ОАН и равен углу QDH. Соответственные углы при пересечении прямых ОН и QD секущей АD равны, следовательно. ОН||QD.
Противоположные стороны четырёхугольника DQOH попарно параллельны, следовательно, DQOH — параллелограмм.
2)
Продолжим боковые стороны трапеции до пересечения в т.М. Углы при основании равнобедренной трапеции равны. Следовательно,
угол АМD=180°-2•75°=30°
Проведем ОК в точку касания. Радиус, проведенный в точку касания, перпендикулярен касательной.
∠ МКО=90°
В прямоугольном ∆ МОК катет ОК противолежит углу 30°, ⇒
гипотенуза МО=2ОК. Т.к. ОК=ОВ=R, МО=2 R.
Тогда MA=3R .
BC║OQ║AD ⇒ ∆BMC~∆ AMD. k=AM:BM=3 ⇒
AD=3BC=3 (ед. длины)
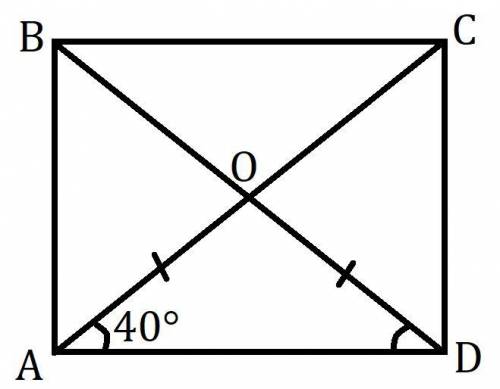
Дан прямоугольник ABCD, ∠CAD:∠CAB=4:5.
Углы прямоугольник равны по 90°.
Пусть ∠CAD=4x, тогда ∠CAB=5x.
∠CAD+∠CAB=∠DAB
4x+5x=9x=90°
x=90°:9=10°
∠CAD=4x=40°
Диагонали в прямоугольнике делятся точкой пересечения пополам.
Пусть AC∩BD=O, тогда AO=DO
В равнобедренном ΔAOD (O-вершина) углы при основании равны. ∠ODA=∠OAD=40°. Сумма углов в треугольнике равна 180°. Откуда ∠AOD=180°-∠ODA-∠OAD=180°-40°-40°=100°
∠AOD>90° ⇒ угол между диагоналями это ∠AOB, смежный с ∠AOD.
∠AOB=180°-∠AOD=180°-100°=80° по свойству смежных углов.
ответ: 80.
Если прямые параллельны, то угловые коэф. равны k=7.
Запишем уравнение окр. в стандартном виде. Для этого в данном уравнении выделим полные квадраты:
x^2+y^2-10x-2y+20=0
(x^2-10x+25) +(у^2-2y+1) - 6=0
(х-5)^2+(у-1)^2=6,
Центр окружности (5; 1)
Уравнение прямой y=kx+b, подставим известные значения для определения b.
7×5+b=1, b=-34.
Искомое уравнение у=7х-34