Формула вычисления стороны квадрата, зная описанный радиус: 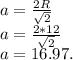
Формула вычисления радиуса вписанной окружности в квадрат, зная его сторону:
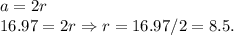
Вывод: Сторона квадрата равна: 16.97; радиус вписанной окружности — 8.5.
8.Формула вычисления радиуса описанной окружности, зная сторону правильного треугольника:
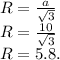
Длина круга равна:
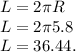
Не поняла, площадь какого круга надо найти, так что найду площади и вписанной, и описанной окружности.
Формула вычисления площади описанной окружности такова:
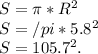
Формула вычисления площади вписанной окружности такова: 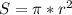
Радиус вписанной окружности в правильный треугольник, мы найдём по стороне этого же треугольника:
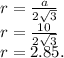
Площадь окружности равна:
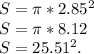
Формула вычисления стороны правильного треугольника, зная радиус описанной окружности:
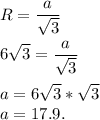
Радиус вписанной окружности равен:
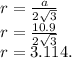
Площадь окружности равна:
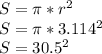
1) 150.
2) 15.
3) 18.
4) 270.
Объяснение:
Площадь трапеции определяется по формуле:
S=h(a+b)/2;
1) a=9+12=21; b=4; h=12.
S=12*(21+4)/2=6*25=150;
***
2) S=h(a+b)/2; a=3; b=9; h=? Высота (катет )лежит против угла в 30* и равна половине гипотенузы h=5/2=2.5;
S=2.5(3+9)/2;
S=2.5*12/2;
S=2.5*6=15.
***
3) Вероятно это равнобокая трапеция и углы при основаниях равны.
Проведем высоту из вершины тупого угла. Получим равнобедренный треугольник с углами по 45*, стороны которых (и высота) равны 9-2*3=9-6=3;
S=h(a+b)/2; h=3; a=3; b=9;
S=3(3+9)/2=3*12/2=18.
***
4) Все величины для нахождения площади известны.
S=h(a+b)/2; h=15; a=4; b=8+24=32;
S=15(4+32)/2;
S=15*36*2=15*18=270.
АС=ВС=> треуг. АВС-равнобедренный=> угол А=В=(180-100):2=40
ответ: 40