ответ: во вложении Объяснение:

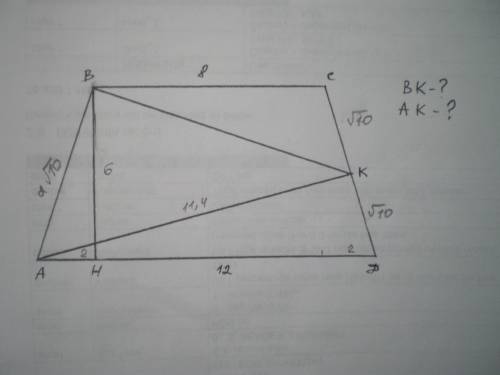
Дано: АВСД - трапеция, АВ=СД, ВС=8 см, АД=12 см, ВН - высота, ВН=6 см, СК=КД. Найти ВК и АК.
Решение: рассмотрим треугольник АВН - прямоугольный.
АН=(АД-ВС):2=2 см
АВ=СД=√(36+4)=√40=2√10 см.; СК=КД=2√10\2=√10 см.
cosA=АН\АВ=2\2√10=√10\10; cosД=√10\10
Рассмотрим треугольник АКД и найдем АК по теореме косинусов:
АК²=АД²+КД²-2*АД*КД*√10\10=144+10-2*12√10*√10\10=130; АК=√130=11,4 см.
Рассмотрим треугольник ВКС и найдем ВК по теореме косинусов:
ВК²=ВС²+СК²-2*ВС*СК*(cos180-α)=64+10-2*8*√10*(-√10\10)=74+16=90;
ВК=√90=9,48 см.
ответ: 11,4 см, 9,48 см.
1) Центр окружности (x+3)²+(у-1)²=R² находится в точке С(-3,1 ) .
Расстояние от точки С(-3,1 ) до оси ОУ равно 3.
Чтобы окружность касалась оси ОУ, надо чтобы её радиус был равен R=3. ответ: В).
2)
ответ: Г ) .
3)
ответ: Б) .
4) Центр окружности х²+у²=1 находится в точке О(0,0). Центр окружности (х-2)²+(у+2)²=1 находится в точке С(2,-2) .
Расстояние между этими точками равно
ответ: А) .