class Program
{
static void Main(string[] args)
{
string src = " Qwy. ... Asdf.. Lkjdfs A.";
//string dest = ReplaceDots(src, '.', '…', 3);
string dest = ReplaceDots(src, '.', "...", 3);
Console.WriteLine("src:\t" + src);
Console.WriteLine("dest:\t" + dest);
Console.WriteLine();
Console.Write("Press any key for exit ...");
Console.ReadKey(true);
}
//private static string ReplaceDots(string src, char dotCh, char dots, int minDotsCount)
private static string ReplaceDots(string src, char dotCh, string dots, int minDotsCount)
{
StringBuilder dest = new StringBuilder();
int i = 0;
while (i < src.Length)
{
int dotsCount = 0;
while (i < src.Length && src[i] == dotCh)
{
dotsCount++;
i++;
}
if (dotsCount >= minDotsCount)
dest.Append(dots);
else if (dotsCount == 0)
dest.Append(src[i++]);
else
while (dotsCount-- > 0)
dest.Append(dotCh);
}
return dest.ToString(); ;
}
}
#include <iostream>
#include <ctime>
#include <Windows.h>
using namespace std;
int main()
{
SetConsoleCP(65001);
SetConsoleOutputCP(65001);
string word;
int g;
long int t1 = time(NULL);
string n = "0123456789ABCDEFG";
string f = "ty"; // Зачем это нужно, если оно нигде не использовано?
int k = 0;
for (auto a : n)
for (auto a1 : n)
for (auto a2 : n)
for (auto a3 : n)
for (auto a4 : n)
{
word.push_back(a);
word.push_back(a1);
word.push_back(a2);
word.push_back(a3);
word.push_back(a4);
cout << word << endl;
g = word.length(); // тоже что-то мутное зачем длинна слова? она всегда равна 4
word.clear();
// не понял прикола if g == g, это всегда истина. поэтому убрал его
k++;
}
long int t2 = time(NULL);
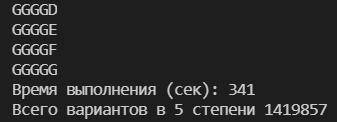
cout << "Время выполнения (сек): " << t2 - t1 << endl; // с выводом слова на экран у меня работает 341 сек ~ 5,5 минут. без - 0 сек
cout << "Всего вариантов в " << g << " степени " << k << endl;
// a = input(":") // Это что вообще? =_= // если хотел чтобы оно не закрывало окно - используй system("pause");
int a;
cout << ":";
cin >> a;
return 0;
}
ответ: 2, 2, 1, 15
Объяснение:
Поскольку переменных всего четыре, можно составить таблицу всех возможных значений (2^4=16) и рассмотреть задачи наглядно. К решению прилагаются картинки.
Задача 1:
Пусть (A v B v C) - X , ( B & C & D) - Y.
Тогда X & Y = 1. Такое может быть только в одном случае, когда и X и Y равны 1. То есть:
(B&C&D) = 1 И (A v B v C) = 1
Для выполнения первого условия необходимо, чтобы все три переменных были 1. Из 16 возможных вариантов остается только 2 (обозначены светло-зеленым). В этих двух вариантах второе условие выполняется автоматически (либо A, либо B, либо C - равны 1).
ответ: 2
Задача 2:
Пусть (A v B v C) - X , ( B & C & D) - Y.
Тогда X v Y = 0. Такое может быть только в одном случае, когда и X и Y равны 0. То есть:
(B&C&D) = 0 И (A v B v C) = 0
Рассмотрим второе условие. Для его выполнения необходимо, чтобы A,B и C были равны нулю. Из 16 возможных вариантов остается 2. Первое условие для этих двух вариантов выполняется автоматически (либо B, либо C, либо D - равны 0).
ответ: 2
Задача 3:
Здесь три скобки, объединенные между собой дизъюнкцией (логическое ИЛИ). Результат равен нулю. То есть ни одна скобка не должна быть равна единице (или все три скобки должны быть равны нулю):
(A -> C) = 0 И (B & A)=0 И (D -> B & C)=0
Рассмотрим третье условие:
(D -> B & C) = 0
У конъюнкции (&) приоритет выше, значит, это первое действие. Вторым будет выполняться импликация. Импликация дает ноль только в том случае, когда левое значение (D) равно единице, а правое нулю. Выделим те варианты, когда это выполняется (светло-зеленым): когда D равно единице, а B&C - нулю (то есть когда одно из них равно нулю).
Далее рассмотрим, когда выполняется второе условие (из уже оставшихся 6 вариантов):
(B & A) = 0 (либо B либо A должны быть равны нулю)
Отметим оставшиеся варианты темно-зеленым.
Осталось первое условие: (A -> C) = 0.
Как мы уже говорили, импликация дает ноль только в том случае, когда левое значение (A) равно единице, а правое (C) - нулю. Оставшийся один вариант отмечен синим.
ответ: 1
Задача 4:
Пусть (A & B & C) - X, (C & D) - Y. Тогда:
X -> Y = 1
В таблице истинности для импликации только один вариант дает ноль. Следовательно, нужно исключить лишь его. Остальные варианты будут решением. Рассмотрим, сколько решений имеет логическое уравнение X -> Y = 0, затем из всех возможных вариантов (16, поскольку 4 переменных) вычтем найденное количество.
Импликация дает ноль только в том случае, когда левое значение (X) равно единице, а правое нулю.
Перепишем условие:
X = 1 И Y =0
(A & B & C) = 1 И (C & D) =0
Первое условие выполняется только в том случае, когда A,B и C равны единице. Таких вариантов два (светло-зеленые). Также либо C либо D должны быть равны нулю. Остается один вариант.
Вспомним, что мы решали обратную задачу. Следовательно, итоговый ответ будет: 16-1=15
ответ: 15
Примечание: решать можно и другими возможно, более простыми. Здесь лишь показан один из путей решения.