Question

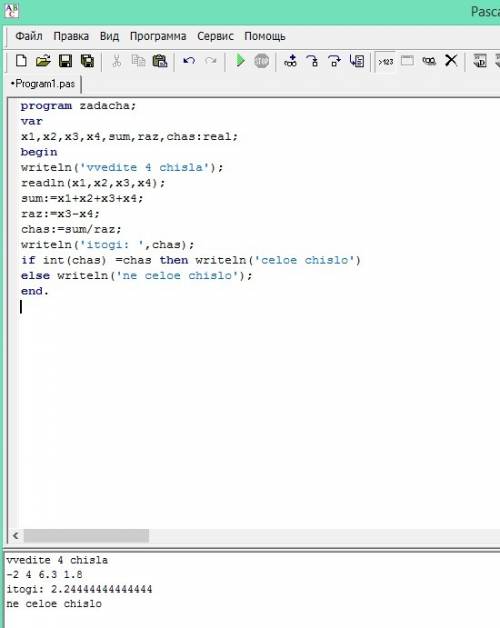
Заполните массив случайными целыми числами от 0 до 99. Выведите исходный массив. Сформируйте новый массив, который бы состоял из элементов первого, записанных справа налево. Выведите его на экран. В отличии от задачи 10, в результате должно быть два различных массива. int[] ms = new int[10];
Random rnd = new Random();
for(int i = 0; i < ms.Length-1; i++)
{
ms[i] = rnd.Next(0, 99);
Console.WriteLine(ms[i] + " ");
}
Console.WriteLine();
int[] ms1 = new int[ms.Length];
for(int i = ms.Length-1; i >= ms1.Length-1; i--)
{
Console.WriteLine(ms1[i] + " ");
}
Что не так?