1. 25 = 5 · 5
65 = 5 · 13
130 = 2 · 5 · 13
Общие множители чисел: 5
НОД (25; 65; 130) = 5
2. 387 = 3 · 3 · 43
198 = 2 · 3 · 3 · 11
Общие множители чисел: 3; 3
НОД (387; 198) = 3 · 3 = 9
3. 25 = 5 · 5
65 = 5 · 13
130 = 2 · 5 · 13
Общие множители чисел: 5
НОД (25; 65; 130) = 5
4. 240 = 2 · 2 · 2 · 2 · 3 · 5
264 = 2 · 2 · 2 · 3 · 11
Общие множители чисел: 2; 2; 2; 3
НОД (240; 264) = 2 · 2 · 2 · 3 = 24
5. 360 = 2 · 2 · 2 · 3 · 3 · 5
432 = 2 · 2 · 2 · 2 · 3 · 3 · 3
Общие множители чисел: 2; 2; 2; 3; 3
НОД (360; 432) = 2 · 2 · 2 · 3 · 3 = 72
6. 36 = 2 · 2 · 3 · 3
90 = 2 · 3 · 3 · 5
108 = 2 · 2 · 3 · 3 · 3
Общие множители чисел: 2; 3; 3
НОД (36; 90; 108) = 2 · 3 · 3 = 18
7. 2 = 2 · 2 · 3
18 = 2 · 3 · 3
72 = 2 · 2 · 2 · 3 · 3
Общие множители чисел: 2; 3
НОД (12; 18; 72) = 2 · 3 = 6
8.
60 = 2 · 2 · 3 · 5
15 = 3 · 5
90 = 2 · 3 · 3 · 5
Общие множители чисел: 3; 5
НОД (60; 15; 90) = 3 · 5 = 15
9. 33 = 3 · 11
21 = 3 · 7
42 = 2 · 3 · 7
Общие множители чисел: 3
НОД (33; 21; 42) = 3
10. 19 = 19
57 = 3 · 19
285 = 3 · 5 · 19
Общие множители чисел: 19
НОД (19; 57; 285) = 19
11. 176 = 2 · 2 · 2 · 2 · 11
144 = 2 · 2 · 2 · 2 · 3 · 3
Общие множители чисел: 2; 2; 2; 2
НОД (176; 144) = 2 · 2 · 2 · 2 = 16
А врать про количество не надо, т.к в задании пишется сколько ты получишь )
Положение вершины параболы определяется по формуле:
хо = -в/2а.
Подставим коэффициенты из заданного уравнения.
хо = -(-2(а+1))/2*1 = а + 1.
Отсюда параметр а = хо - 1.
Чтобы вершина была правее оси Оу, значение хо должно быть положительным. То есть хо = а + 1 > 0.
Отсюда a > -1.
Далее, чтобы вершина была выше оси Ох, значение у должно быть больше 0: x²-2(a+1)x+(2018/a) > 0.
D = 4(a+1)² - 4*1*(2018/a) = 4a² + 8a + 4 - (4072/a).
Чтобы вершина была выше оси Ох надо, чтобы дискриминант был меньше 0: 4a² + 8a + 4 - (4072/a) < 0.
Получаем выражение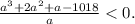
Из него получаем a < 9,4043.
С учётом, что а не равно 0, получаем ответ.
ответ: -1 < a < 0, 0 < a < 9,4043.