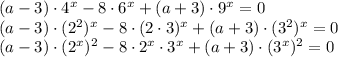
Для удобства произведём замену переменных:
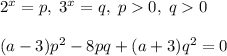
Рассмотрим последнее уравнение как квадратное в отношении переменной p (можно и в отношении q - результат будет тот же). Оно не будет иметь корней, если его дискриминант будет отрицательным.
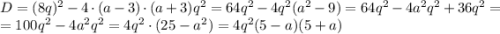
Решение задачи сводится к решению неравенства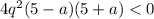 
. Очевидно, что множитель 4q² будет положительным при любых q≠0. Однако ранее мы определили, что q>0, значит этот множитель не влияет на неравенство, и мы можем его отбросить.
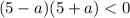
Получаем три интервала для a: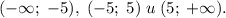 
Проверив знаки на каждом интервале, получим, что последнее неравенство выполняется при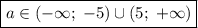 
.
В начале было 400 000 руб.
в конце года стало 450000 руб. (400000+12,5%)
в конце второго года стало 506 250 руб.
в начале второго стало 507250( т.к. Егор Николаевич увеличил допустим на 1000)
в конце третьего года стало 570 656 руб.
в начале четвертого года стало 571656
в конце четвертого стало 643 113 руб.
№1. Если возьмём , что т =2 , то в конце получится
645503, что неверно.
( Я считала очень много и в конце получилось число 25)
Если взять, что т-25, то получится 700422 руб. , что и является наименьшим
ответ: 25