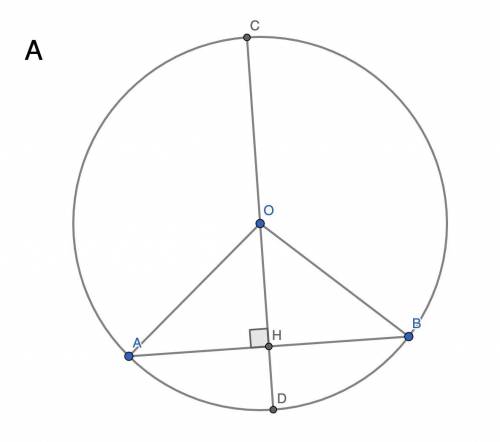
А. Пусть дана окружность с центром O и радиусом R, хордой AB, диаметром CD, перпендикулярным хорде и пересекающим его в точке H. OA = OB = R ⇒ OAB — равнобедренный треугольник. OH — его высота, а значит, медиана ⇒ AH = HB, ч. т. д.
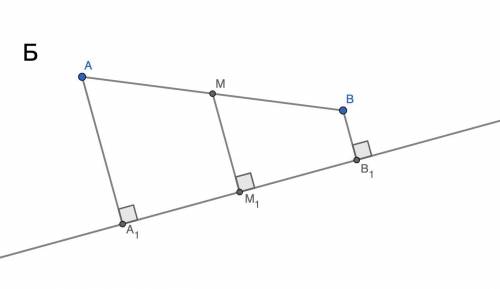
Б. Так как AA₁, BB₁, MM₁ перпендикулярны одной прямой, они друг другу параллельны. По теореме Фалеса так как AM = MB, A₁M₁ = M₁B₁, ч. т. д.
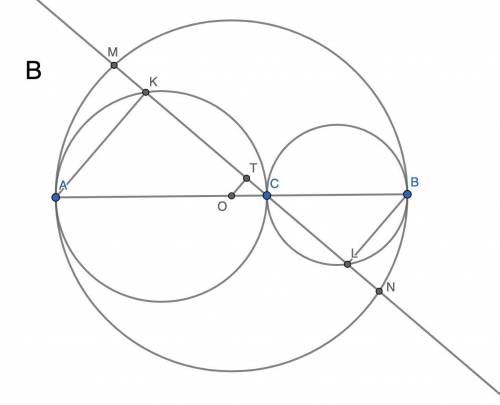
В. Заметим, что изменение положения точек M и N изменяет длину каждого из отрезков KM и LN на длину KL, что не влияет на факт равенства, поэтому достаточно доказать только конфигурацию, представленной на рис. 3. Пусть O — середина AB. Спроецируем О на MN в точку T. OT — часть диаметра, OT⊥MN, тогда по задаче А MT = TN. AO = OB, тогда по задаче Б KT = TL. Тогда KM = TM - TK = TN - TL = LN, ч. т. д.
Отношение оснований BC и AD трапеции ABCD равно 1 : 5. Точка Е и K находятся на стороне CD и делят ее в отношене 1:2:1. Точка F делит сторону АВ пополам. Найдите отношение площади трапеции на площадь треугольника EFK.
Проведём среднюю линию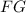
. Средняя линия трапеции делит её высоту пополам и обозначим 
, 
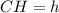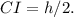
Пусть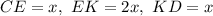
тогда, E — середина отрезка CG и точка G — середина отрезка EK (т.к. EG = GK = 2x - x = x). Следовательно, 
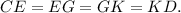Обозначим 
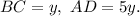Определим отношение площадей трапеций ABCD и FBCG
Определим отношение площадей трапеции FBCG и треугольника FEG
Поскольку G — середина EK, то FG — медиана треугольника FEK и делит она площадь треугольника пополам.
Выразив отсюда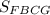
и подставив в равенство (1), мы получим
ответ: 4 : 1.