Удвух мальчиков было 34ман. первый из них потратил 75% своих денег а во второй день потратил 5/6 своих денег после этого у них осталось 7 манат сколько денег было у каждого мальчика

👇

Увидеть ответ

Ответ:

6jytu

29.11.2022

75% = 75/100 = 3/4 - сократили на 25

Пусть х манат было у одного мальчика, тогда (34 - х) манат - у другого. Уравнение:

3/4 · х + 5/6 · (34 - х) = 34 - 7

(3/4)х + 170/6 - (5/6)х = 27

(3/4)х - (5/6х) = 27 - 85/3

(9/12)х - (10/12)х = 27 - 28 целых 1/3

(-1/12)х = - 1 целая 1/3

х = - 4/3 : (-1/12)

х = 4/3 · 12/1

х = 48/3

х = 16 (манат) - было у одного мальчика

34 - 16 = 18 (манат) - было у другого мальчика

ответ: 16 манат и 18 манат.

Проверка:

1) 3/4 · 16 = 16 : 4 · 3 = 12 манат потратил первый мальчик

2) 5/6 · 18 = 18 : 6 · 5 = 15 манат потратил другой мальчик

3) 34 - (12 + 15) = 7 манат - столько денег у них осталось

4,5(61 оценок)

Открыть все ответы

Ответ:

veronikamihailova37

29.11.2022

Найдем производную, приравняем ее к нулю. найдем критические точки, разобьем область определения функции на промежутки и установим знак на каждом из них. где производная больше нуля - там функция возрастает, где она меньше нуля. функция убывает. при переходе через критическую точку : если производная меняет знак с плюса на минус, то это точка максимума, с минуса на плюс - точка миниимума, а значения функции в этих точках - соответственно максимум и минимум.

f'(x)=(x³/3+x²-3x-1)'=x²+2x-3

x²+2x-3=0 По Виету х=-3, х=1, неравенство решим методом интервалов (х+3)(х-1)<0

-31

+ - +

На промежутках (-∞;-3] и [1;+∞) функция возрастает, а на

[-3;1] убывает. Точка х= -3 - точка максимума, а х=1- точка минимума, максимум равен -27/3+9+9-1=8; минимум равен

1/3+1²-3-1-2 2/3

4,6(81 оценок)

Ответ:

drazzgaming

29.11.2022

1) Находим область определения: вся числовая ось, кроме х = -5 / 4 (при этом значении знаменатель превращается в ноль).
2) Находим точки пересечения с осями:
х = 0 у = -3/5 это точка пересечения с осью у.
у = 0 надо числитель приравнять 0: 2х - 3 = 0 х = 3/2 это точка пересечения с осью х.
3) Исследуем функцию на парность или непарность:
Функция называется парной, если для любого аргумента с его областью обозначения будет f(-x)=f(x), или же непарной - если для любого аргумента с областью обозначения будет f(-x)=-f(x). К тому же, график парной функции будет симметричным относительно оси ординат, а график непарной - симметричным относительно точки (0;0).
Правда, чаще встречается название этих свойств функции как чётность и нечётность.
2*x - 3 -3 - 2*x ---------- = ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет 2*x - 3 -3 - 2*x ---------- = - ---------- 1 1 (4*x + 5) (5 - 4*x) - Нет, значит, функция не является ни чётной, ни нечётной.
4) Исследуем функцию на монотонность: — это значит выяснить, на каких промежутках области определения функция возрастает, а на каких убывает.
Если производная положительна, то функция возрастает и наоборот.
$\frac{d}{dx} ( \frac{2x-3}{4x+5} )= \frac{22}{(4x+5)^2}$ .
Так как переменная в квадрате, то производная всегда положительна, а функция возрастающая на всей числовой оси (кроме х = -5/4).
5) Находим экстремумы функции:
Так как переменная находится в знаменателе, то производная не может быть равна нулю. Следовательно, функция не имеет ни максимума, ни минимума.
6) Исследуем функции на выпуклость, вогнутость:
Если вторая производная меньше нуля, то функция выпуклая, если производная больше нуля - то функция вогнутая.
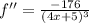Вторая производная равна $f''= \frac{-176}{(4x+5)^3}$ .
При x > (-5/4) функция выпуклая, при x < (-5/4) функция вогнута.
7) Находим асимптоты графика функции:
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo 2*x - 3 lim ------- = 1/2 x->-oo4*x + 5 значит,уравнение горизонтальной асимптоты слева:y = 1/2 2*x - 3 lim ------- = 1/2 x->oo4*x + 5 значит,уравнение горизонтальной асимптоты справа:y = 1/2Наклонные асимптотыНаклонную асимптоту можно найти, подсчитав предел функции (2*x - 3)/(4*x + 5), делённой на x при x->+oo и x->-oo 2*x - 3 lim ----------- = 0 x->-oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой справа 2*x - 3 lim ----------- = 0 x->oox*(4*x + 5) значит,наклонная совпадает с горизонтальной асимптотой слева
8) Можно найти дополнительные точки и построить график
График и таблица точек приведены в приложении.
1. исследовать функцию и построить график y(x)=(2x-3)/(4x+5) огромная решить , которое выполняется с