Наименьшее трехзначное число, делящееся на 13 это 104, а наибольшее — 988. Мы имеем последовательность трёхзначных чисел, делящихся на 13. Эта последовательность - арифметическая прогрессия с первым членом 104 и разностью прогрессии d = 13.
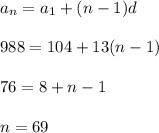
Т.е. всего 69 трёхзначных чисел, делящихся на 13.
Всего трёхзначных чисел: 999 - 99 = 900.
Вероятность того, что наугад выбранное трёхзначное число делится на 13 равна 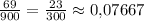

x y z B 42 Определитель
5 -1 1 -3
-1 3 1 -1
2 1 4 1
Заменяем 1-й столбец на вектор результатов B:
-3 -1 1 -42 Определитель
-1 3 1
1 1 4
Заменяем 2-й столбец на вектор результатов B:
5 -3 1 -42 Определитель
-1 -1 1
2 1 4
Заменяем 3-й столбец на вектор результатов B:
5 -1 -3 42 Определитель
-1 3 -1
2 1 1
x = -42 / 42 = -1
y = -42 / 42 = -1
z = 42 / 42 = 1.
Определители проще находить методом "параллельных полосок".
Вот первый из них.
5 -1 1| 5 -1
-1 3 1| -1 3
2 1 4| 2 1 =
= 60 -2 -1 - 4 - 5 - 6 = 42.
Решение задания прилагаю