
1) Позвольте рассуждать так: выражение в скобках, возведённое в квадрат(по условию задания) всегда, при любых положительных или отрицательных числах значения х, будет положительным числом. А тут к тому же второе слагаемое 4 также положительно. Что не оставляет нам выбора, как только выяснить, какое наименьшее значение будет в скобках.
2)Теперь вопрос, а какое число считать наименьшим среди положительных чисел?( смело будем считать, что это число 0, т.к оно не относится ни к отрицательным ни к положительным числам).
3) Тогда чтобы получить в выражении в скобках 0, надо чтобы х=5
4) Итак (5-5)²+4=0+4=4
Пошаговое объяснение:
Преобразуем: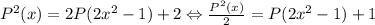 . Сделаем замену:
. Сделаем замену:  (полином имеет значение в любой точке), тогда:
(полином имеет значение в любой точке), тогда: 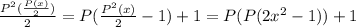 . Отсюда:
. Отсюда:  , поскольку
, поскольку  . Пусть
. Пусть  обозначает примененную
обозначает примененную  раз композицию функции
раз композицию функции  с самой собой. Аналогичным образом связана функция
с самой собой. Аналогичным образом связана функция  с функцией
с функцией  . Продолжая вышеуказанные подстановки, приходим к равенству
. Продолжая вышеуказанные подстановки, приходим к равенству  . Теперь:
. Теперь:  , поскольку
, поскольку  (здесь
(здесь 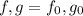 ). Но
). Но  , значит,
, значит,  , но старший коэффициент
, но старший коэффициент  положителен, откуда
положителен, откуда  . Пусть старший коэффициент
. Пусть старший коэффициент  равен
равен  . Предположим, что
. Предположим, что  . Посчитаем старший коэффициент слева:
. Посчитаем старший коэффициент слева:  , где
, где  — степень многочлена
— степень многочлена  . Старший коэффициент справа равен старшему коэффициенту
. Старший коэффициент справа равен старшему коэффициенту  и равен
и равен  . Приравниваем:
. Приравниваем:  (поскольку
(поскольку  ). В частности,
). В частности,  .
.
Заметим, что старший коэффициент равен
равен  (в этом несложно убедиться). Тогда
(в этом несложно убедиться). Тогда  , но такого натурального
, но такого натурального  нет. Стало быть,
нет. Стало быть,  , то есть
, то есть  константа. Пусть
константа. Пусть  :
:  .
.