Р 259. Древнегреческих, а также древнеиндийских ма-
тематиков интересовали числа, которые соответствова-
ли котичеству точек, расположенных в виде некоторой
геометрической фигуры треугольника. Квадрата и др.
Такие чиста называли фигурными. Например, число 10
называли треугольным, число 16 — квадратным (рис. 13).
Такое представление древним ученым изучать
свойства чисел. Используя рисунок 13, попробуйте най-
тін еще несколько треугольных и квадратных чисел. Ка-
кими свойствами обладают этих числа? Подумайте, как
можно находить треугольные и квадратные числа, ис-
пользуя ряд натуральных чисел.
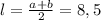, то можно найти длину АК: 
.
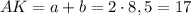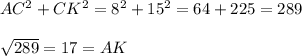
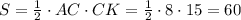
n/m≤200/101<2 - противоречие) Таким образом, каждый наибольший нечетный делитель числа из диапазона от 101 до 200 не превосходит 200, все они различны, их 100 штук, а значит они - все нечетные числа в диапазоне от 1 до 200 (их тоже 100 штук). Значит искомая сумма равна сумме всех нечетных чисел от 1 до 200, т.е. (1+199)·100/2=10000.