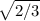Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R Знаю только то что в решении используются производные ...
Посмотрим на шар сбоку (см. рис). Тогда цилиндр мы будем видеть как прямоугольник. Пусть, a - диаметр круга в основании цилиндра, b - высота цилиндра. Тогда объем цилиндра вычисляется по формуле
V = pi * (a/2)² * b = (pi/4) * a²b
Чтобы объем был максимальным, нужно, чтобы величина a²b была максимальной. Заметим, что a² = c²-b² = 4R² - b²
max(a²b) = max((4R²-b²)*b)
Пусть, f(b) = (k-b²)*b, где k = 4R².
Эта функция имеет график, как на рисунке, т.е. проходит через точку (0;0). Нас интересует максимум при b>0. Он достигается в точке, где f'(b) = 0.
f'(b) = k - 3b² = 0.
b = +-
b = - не подходит, т.к. b положительно.
Значит, b = = R * 2/
a = = = R * 2, радиус основания в 2 раза меньше, т.е. R*
Наибольший общий делитель:: Разложим числа на простые множители и подчеркнем общие множители чисел:252 = 2 · 2 · 3 · 3 · 7441 = 3 · 3 · 7 · 71080 = 2 · 2 · 2 · 3 · 3 · 3 · 5 Общие множители чисел: 3; 3 Чтобы найти НОД чисел, необходимо перемножить их общие множители: НОД (252; 441; 1080) = 3 · 3 = 9
Наименьшее общее кратное:: Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.360 = 2 · 2 · 2 · 3 · 3 · 570 = 2 · 5 · 7Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их: НОК (360; 70) = 2 · 2 · 2 · 3 · 3 · 5 · 7 = 2520 Наименьшее общее кратное:: Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.180 = 2 · 2 · 3 · 3 · 572 = 2 · 2 · 2 · 3 · 3Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их: НОК (72; 180) = 2 · 2 · 3 · 3 · 5 · 2 = 360
Сначала мы видим есть остаток и нет неполного делимого чтоб всё было легко нам надо первый поимер 1)60200-200=60000-мы просто от делимого отняли остаток. 2)60000:6=10000-всё проверка: 10000*6=60000 60000+200=60200 значит: 60200:10000=6(ост.200) второй пример 1)5608-8=5600 2)5600:100=56. проверка: 56*100=5600 5600+8=5608 значит: 5608:56=100(ост.8) третьи пример 1)34052-52=34000 2)34000:34=1000 проверка: 1000*34=34000 34000+52=34052 значит: 34052:1000=34(ост.52) четвёртый пример 1)80710-10=80700 2)80700:807=100 проверка: 100*807=80700 80700+10=80710 значит: 80710:100=807(ост.10) пятый пример 1)24385-5=24380 2)24380:2438=10 проверка: 2438*10=24380 24380+5=24385 значит: 24385:10= 2438(ост.5)
Радиус основания = R*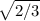
, высота = R * 2/
.
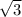Пошаговое объяснение:
Посмотрим на шар сбоку (см. рис). Тогда цилиндр мы будем видеть как прямоугольник. Пусть, a - диаметр круга в основании цилиндра, b - высота цилиндра. Тогда объем цилиндра вычисляется по формуле
V = pi * (a/2)² * b = (pi/4) * a²b
Чтобы объем был максимальным, нужно, чтобы величина a²b была максимальной. Заметим, что a² = c²-b² = 4R² - b²
max(a²b) = max((4R²-b²)*b)
Пусть, f(b) = (k-b²)*b, где k = 4R².
Эта функция имеет график, как на рисунке, т.е. проходит через точку (0;0). Нас интересует максимум при b>0. Он достигается в точке, где f'(b) = 0.
f'(b) = k - 3b² = 0.
b = +-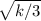
b = -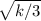
не подходит, т.к. b положительно.
Значит, b =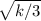
= R * 2/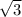
a =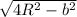
= 
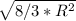= R * 2
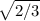, радиус основания в 2 раза меньше, т.е. R*