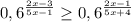
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
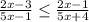
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
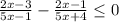
Приводим к общему знаменателю и получаем неравенство
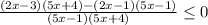
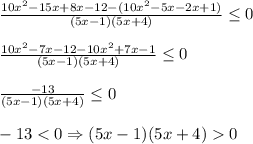
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
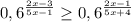
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
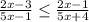
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
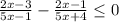
Приводим к общему знаменателю и получаем неравенство
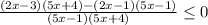
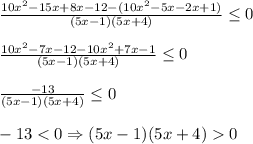
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
То, что решается через характеристическое уравнение - это общее решение. Оно всегда будет независимо от правой части диффура.
По сути, нужно найти так называемое частное решение, и тогда решением для этого диффура будет сумма общего и частного решений.
Частное решение подбирается, исходя из правой части. В данном случае, правая часть есть многочлен второго порядка. Поэтому частное решение будет также иметь вид многочлена, причем многочлена второго порядка: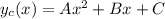 (
(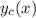 - частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
- частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
(второго порядка потому, что многочлена первого порядка может не хватать, а многочлен не ниже третьего порядка избыточен, можешь попробовать подставить многочлен третьего порядка, но при нахождении коэффициентов он занулится)
UPD: ошибся в выборе многочена. Нужно использовать многочлен третьего порядка: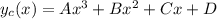 (необходимо, чтобы после подстановки
(необходимо, чтобы после подстановки 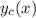 в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)
в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)