Пошаговое объяснение:
приведем квадратичную форму
B = x² + 9y²
к главным осям, то есть к каноническому виду
матрица этой квадратичной формы
1 0
0 9
собственные числа и собственные векторы этой матрицы
(1 - λ)x + 0y = 0
0x + (9 - λ)y = 0
характеристическое уравнение
λ² - 10λ + 9 = 0
D=(-10)² - 4*1*9=64
λ₁ = 9; λ₂ = 1
поскольку λ₁ > 0; λ₂ > 0, это эллипс
квадратичная форма
х² +9у²
выделим полные квадраты
для х
(x²-2*20x + 20²) -1*20² = (x-20)²-400
для y
9(y²+2*2y + 2²) -9*22 = 9(y+2)²-36
и получим
(x-20)²+9(y+2)² = 336
делим все на 336
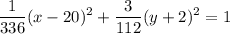
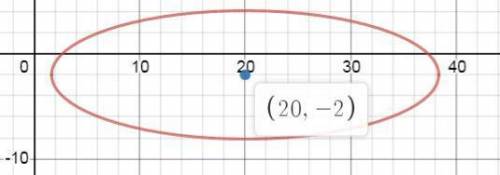
эллипс с центром в точке С(20; -2)
полуоси

фокусы
координаты фокусов F₁(-c;0) и F₂(c;0), где c - половина расстояния между фокусами
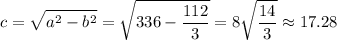
и тогда фокусы
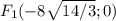
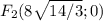
с учетом центра фокусы будут
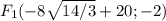
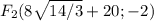
Гюз гелди, гетди къушлар,
Ана ватанын къоюп.
Гюнеш шавласын яймай,
Гечелер къысгъа болуп.
Йылны заманларындан мен гюзню сюемен. Озокъда, къыш да арив оьзюню тазалыгъы, акълыгъы булан. Язбашда да, янгы юхудан уянгъан къызъяшдай, табиат уяна, авлакълар яшыл от булан, бавлар чечеклер булан безенелер. Тек гюзню адам тергевлю къарамаса эс де этмес йимик аламатлары кёп бар.
Гюзню гюню… Тунукъ кёкдеги булутланы артындан гюнеш, чубулдурукъну артындан яшынып-яшынып къарайгъан гелин йимик, уялчан къарай. Ел уьфюрюп тереклердеги ахырынчы япыракъланы юлкъуп ата, япыракълар оьзлер терекден даимге айрылгъанына инанма болмай, гьавада саркъып, ерде рагьатлыкъ таба. Себелейген увакъ янгур тереклени ялангъач къаркъараларындан четимсиз агъа. Терек тюпдеги къызыл, сари, боямыш япыракълардан бир тамаша хали согъулгъан деп эсинге геле. Оланы уьстюндеги янгурну тамчылары, ойлу гёзден тюшюп битмеген гёзьяш йимик йыртыллай. Исси якълагъа учуп барагъан къушланы пашман йыры адамны юрегин титирете. Гюзню гёзел пашманлыгъы адамны гёнгюн пашман этсе де, язбаш гелип, табиат янгыдан яшнажакъ деген умут юрекни сёнме къоймай.
Объяснение: