Из знаменателя нам нужно только взять ограничение подкоренного выражения, которое и будет являться областью определения неравенства (в числителе ограничений нет):
Помним про это.
Теперь решаем само неравенство
- это нам потребуется
Заметим, что для любых , поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.
Чтобы решить полученное неравенство методом интервалов, найдем нули выражения, стоящего левее знака:
Замечательно, теперь ничего не мешает использовать метод интервалов. Заметим, что функция, у которой мы нули находили - четная, так как везде с иксами модули стоят, поэтому , и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.
На обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).
На (можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:
, первая скобка отрицательна, вторая положительна, то есть выражение отрицательно (-).
Теперь симметрично отображаем и получаем на отрицательно (-)
А на положительно (+).
То есть надо было бы взять , не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое
Накладывая ограничение, получим итоговый ответ:
То есть это самый последний, 5-ый ответ из тех, что можно выбрать.
Это? Расхвастался как-то Глагол перед Именем существительным:— Я среди Частей речи самый главный. Я у самого Юлия Цезаря в почёте был! «Пришёл! Увидел! Победил!» — этими словами знаменитый полководец выразил всё, что хотел сказать. Заметьте: три глагола, три сказуемых, и ни одного существительного!— Скажешь тоже! — обиделось Существительное. — Я тебя лучше, потому что я — всё! Моим именем названо всё, что тебя окружает: все предметы и звери, и птицы, и люди, и даже мы с тобой — словом, всё-всё-всё! Выходит, я – главнее тебя, да и всех остальных тоже.— О чём это Вы так жарко спорите? — спросило мимо проходящее Прилагательное.— О том, кто из нас главнее! — ответили Глагол и Существительное.— Почему это Вы так решили, ребята, что Вы — лучшие? Я, и только я лучшая часть речи! Я — вся красота, вся радость, все цвета, всё настроение этого мира! Без меня Вы не узнаете, каким ласковым может быть солнце, каким ярким – день, какой зелёной – трава, какой доброй – мама.Услышав это, сбежались все части речи: и наречие, и предлог, и числительное — и начали спорить и доказывать друг другу то, что они – самые лучшие и самые важные Части речи.— Глупенькие детки!- вдруг сказало откуда ни возьмись старый дедушка Местоимение. — Глупенькие малые детки! Все Вы одинаково важны и хороши собой! Без тебя, Имя существительное, все предметы остались бы без имени, без тебя, Глагол, невозможно было бы обозначить действие, а без тебя, Имя прилагательное, предметы, действительно, потеряли бы все краски и качества. Но каждый из Вас друг без друга выглядит сиротливо, одиноко и недосказано.Задумались тут Части речи. А ведь правда, мало могут рассказать они о мире поодиночке и поняли, что старый дедушка Местоимение прав.— А ты, дедушка, тоже для чего-то нужен в речи?— Конечно, — ответило Местоимение, — я иногда заменяю Вас по необходимости, когда Вы сильно устаёте или слов Вашей Части речи становится очень много. Вот, например, такой текст:«В углу стоял стол. На столе стояла ваза с цветами. Около стола – стул. Под столом – табуретка».Ну, как Вам рассказ?— Что-то много уж раз повторяется слово «стол», — заметили Части речи.— Вот именно, в таких случаях прихожу на я, Местоимение. И текст получается другим:«В углу стоял стол. На нём стояла ваза с цветами. Около него – стул. Под столом – табуретка».Вот теперь, когда появилось местоимение «ОН», рассказ звучит лучше?- спросил дедушка Местоимение.— Да, это так, — согласились Части речи.Тогда все Части речи помирились и больше никогда не ссорились друг с другом. Ведь если поссорятся все Части речи, разве красивой и правильной будет наша речь?
Из знаменателя нам нужно только взять ограничение подкоренного выражения, которое и будет являться областью определения неравенства (в числителе ограничений нет):
Помним про это.
Теперь решаем само неравенство
Заметим, что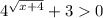 для любых
для любых  , поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.
, поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.
Чтобы решить полученное неравенство методом интервалов, найдем нули выражения, стоящего левее знака:
Замечательно, теперь ничего не мешает использовать метод интервалов. Заметим, что функция, у которой мы нули находили - четная, так как везде с иксами модули стоят, поэтому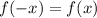 , и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.
, и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.
На обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).
обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).
На (можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:
(можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:
Теперь симметрично отображаем и получаем на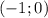 отрицательно (-)
отрицательно (-)
А на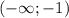 положительно (+).
положительно (+).
То есть надо было бы взять![x\in(-\infty;-1]\cup \{0\} \cup [1;+\infty)](/tpl/images/1255/7524/6fdfe.png) , не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое
, не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое 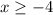
Накладывая ограничение, получим итоговый ответ:
То есть это самый последний, 5-ый ответ из тех, что можно выбрать.