Пошаговое объяснение:
1) Координаты середины отрезка - это среднее арифметическое от координат концов отрезка.
C( (-3+5)/2 ; (-4-2)/2 ) = (2/2; -6/2) = (1; -3)
2) Радиус окружности - это расстояние между ее центром и точкой B.
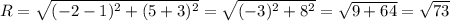
Уравнение окружности
(x-x0)^2 + (y-y0)^2 = R^2, где (x0; y0) - координаты точки О.
(x-1)^2 + (y+3)^2 = 73
3) Точка М сдвинута от точки N на такое же расстояние и в том же направлении, как точка F от точки К.
F(K-2; K-1) = (8-2; -1-1) = (6; -2)
M(N-2; N-1) = (5-2; 5-1) = (3; 4)
ответ: M(3; 4)
4) Уравнение прямой по двум точкам
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
(x + 3)/(2 + 3) = (y - 15)/(-1 - 15)
(x + 3)/5 = -(y - 15)/16
Это каноническое уравнение.
Можно преобразовать в общий вид ax + by + c = 0
16(x + 3) = -5(y - 15)
16x + 48 = -5y + 75
16x + 5y - 27 = 0
Или в вид с угловым коэффициентом y = kx + b
5y = -16x + 27
y = -16x/5 + 27/5
5) Нужно найти точку на оси ординат, то есть x = 0, которая лежит на одинаковом расстоянии от точек М и N. Это точка А(0; y)
|AM| = |AN|
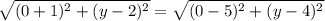
Избавляемся от корней и раскрываем скобки
1 + y^2 - 4y + 4 = 25 + y^2 - 8y + 16
Приводим подобные
8y - 4y = 36
y = 36/4 = 9
ответ: (0; 9)
6) Если прямые параллельны, то коэффициенты при х одинаковы.
Уравнение имеет вид: y = 7x + b
Теперь окружность. Приведем уравнение к обычному виду.
x^2 + y^2 - 10x - 2y + 20 = 0
(x^2 - 10x + 25) - 25 + (y^2 - 2y + 1) - 1 + 20 = 0
(x - 5)^2 + (y - 1)^2 = 6
Центр этой окружности O(5; 1)
Уравнение прямой (x - 5)/1 = (y - 1)/7
7(x - 5) = y - 1
y = 7x - 35 + 1
ответ: y = 7x - 34
1)2(х+3у)+9=х+6
3(х-2у)=х+30
2x+6y+9=x+6
3x-6y=x+30
x+6y+3=0
2x-6y-30=0
3x-27=0
3x=27
x=9
9+6y+3=0
6y=-12
y=-2
(9;-2)
2) 5(3х+2)=7+12у
4(х+у)+х=31
15x+10=7+12y
4x+4y+x=31
15x-12y=-3
5x+4y=31 |*3
15x-12y=-3
15x+12y=93
30x=90
x=3
45+12y=93
12y=48
y=4
(3;4)
3)4(3х+у)-1=у-2х
2(4х-у)+19=-х
12x+4y-1=y-2x
8x-2y+19=-x
14x+3y=1 | *2
9x-2y+19=0 |*3
28x+6y=2
27x-6y=-57
55x=-55
x=-1
-14+3y=1
3y=15
y=5
(-1;5)
4) 2(х+2у)-7у=6
5(2х+у)-х=2у+60
2x+4y-7y=6
10x+5y-x=2y+60
2x-3y=6
9x+3y=60
11x=66
x=6
12-3y=6
-3y=-6
y=2
(6;2)