AD = 12
Пошаговое объяснение:
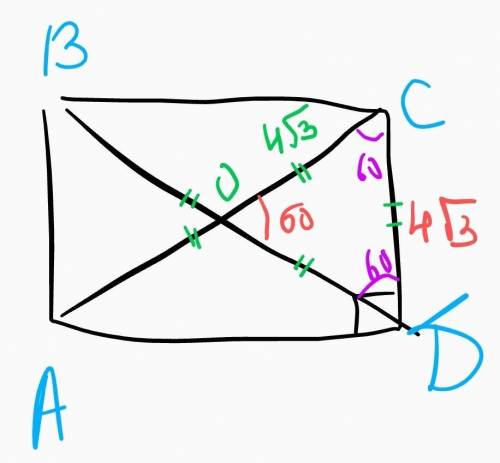
Дано: ABCD - прям.; ВD ∩ AC = O; <COD = 60°; CD = 4√3
Найти: АD
Т.к. т. О - т. пересечения диаг. АС и BD => СО = OD = BO = OD (по св-ву прям.)
Раз CO = OD => ∆COD - р/б => <ОСD = <CDO
<OСD = <CDO = (180° - <COD)/2
<ОСD = <CDO = 60°
<OCD = <CDO = <COD = 60° => ∆OCD - р/с => CO = CD = 4√3
Раз CO = OA (по док. выше) => АС = 2СО => АС =8√3
т.к ∆CDA - п/у => CD² + AD² = AC² (по теореме Пифагора)
AD² = AC² - CD²
AD² = 64*3 - 16*3
AD² = 144
AD = 12
Перевод.
(Аn) - арифметическая прогрессия, а7 = - 27 а12 = - 47. Найти сумму первых пятнадцати членов этой прогрессии
1)для начала нужно найти разность прогрессии
d=( a12-a7)/5= (-27-(-47))/5 = 20/5 = 4
2)узнаем чему равняется а1:
а1=аn - d*(n-1)= -27 - 4*(7-1) = -27 - 24 = - 51
3)теперь нужно найти пятнадцатый член прогрессии:
а15 = а1 + d*(n-1) = -71 + 4*(15-1) = -51 + 56 = 5
4)находим сумму 15 первых членов арифметической прогрессии:
S15 = (a1 + a15)/2 * 15 = (-51+5)/2 * 15 = -46/2 *15 = -345
Пошаговое объяснение: