Перепишу условие, подставив а = 4.
В урне 4 черных и 5 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того что среди них окажется:
а) 4 белых шаров;
б) не более чем 4 белых шаров.
Общее число возможных элементарных исходов для данных испытаний равно числу которыми можно выбрать 5 шаров из 9:
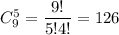
Пусть случайная величина Х — появление белого шара;
Подсчитаем число исходов, благоприятствующих данному событию:
a) Выбрать четыре белых шаров можно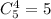 
а один черный шар — 
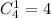По правилу произведения, всего таких
Искомая вероятность: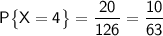 
б) Здесь нужно посчитать вероятность через противоположное событие, то есть:
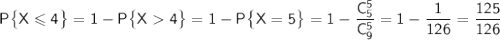
Пошаговое объяснение:
1) - 4 = -0,1х + 2;
0,1х=2+4
0,1х=6
Х=6:0,1
Х=60
3) 4 1/6 - 1 1/3х = 4х+ 3 5/18
-1 1/3х-4х=3 5/18-4 1/6
-5 1/3х=3 5/18-4 3/18
-5 1/3х=-16/18
Х=-16/18:(-5 1/3)
Х=-16/18*(-3/16)
Х=1/6