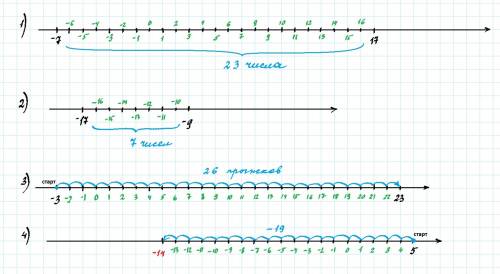
1) На координатном луче отмечаем точки (-7) и (17). Затем отмечаем все точки, лежащие между данными и соответствующие целым числам (смотри рис. 1). Считаем их количество. Получается 23.
Второй И еще из результата (24) вычитаем 1, т.к. одну крайнюю точку - (17) - учитывать не нужно..
24-1 = 23
ответ: 23
2) Чертим координатную прямую и отмечаем на ней точки (-17) и (-9). Затем отмечаем все точки между данными, соответствующие целым числам (см. рис. 2). Считаем их количество. Получается 9 чисел.
Либо можно сосчитать так: -9-(-17) = -9+17 = 8 – это количество чисел от (-17) до (-9), не считая (-17).
Убираем еще одно число, т.к. (-9) тоже не нужно учитывать.
8-1 = 7
ответ: 7
3) Кузнечик стартует в точке (-3), а в точке 23 останавливается.
Все целые числа он должен проходит по порядку. Ему необходимо прыгать только вправо. Тогда количество прыжков будет наименьшим. Если он сделает хоть один прыжок назад, это увеличит общее количество прыжков (см. рис. 3).
В этом случае от (-3) до 23 кузнечик сделает 23-(-3)=23+3=26 прыжков.
ответ: 26
4) Чертим числовую прямую. Отмечаем на ней точки, соответствующие целым числам. От точки (5) отсчитываем 19 целых чисел влево, т.к. нужно вычесть 19.
Оказываемся в точке (-14) (см. рис. 4)
ответ: -14
1) На координатном луче отмечаем точки (-7) и (17). Затем отмечаем все точки, лежащие между данными и соответствующие целым числам (смотри рис. 1). Считаем их количество. Получается 23.
Второй И еще из результата (24) вычитаем 1, т.к. одну крайнюю точку - (17) - учитывать не нужно..
24-1 = 23
ответ: 23
2) Чертим координатную прямую и отмечаем на ней точки (-17) и (-9). Затем отмечаем все точки между данными, соответствующие целым числам (см. рис. 2). Считаем их количество. Получается 9 чисел.
Либо можно сосчитать так: -9-(-17) = -9+17 = 8 – это количество чисел от (-17) до (-9), не считая (-17).
Убираем еще одно число, т.к. (-9) тоже не нужно учитывать.
8-1 = 7
ответ: 7
3) Кузнечик стартует в точке (-3), а в точке 23 останавливается.
Все целые числа он должен проходит по порядку. Ему необходимо прыгать только вправо. Тогда количество прыжков будет наименьшим. Если он сделает хоть один прыжок назад, это увеличит общее количество прыжков (см. рис. 3).
В этом случае от (-3) до 23 кузнечик сделает 23-(-3)=23+3=26 прыжков.
ответ: 26
4) Чертим числовую прямую. Отмечаем на ней точки, соответствующие целым числам. От точки (5) отсчитываем 19 целых чисел влево, т.к. нужно вычесть 19.
Оказываемся в точке (-14) (см. рис. 4)
ответ: -14

Введем обозначения неизвестных величин:
х км/ч - скорость первого пешехода
у км/ч - скорость второго пешехода
t ч - время их движения до встречи.
Тогда t(x+y)=42
Если бы они оба шли с одинаковой скоростью, равной скорости 2-го пешехода, то
(t-1/2)(y+y)=42
Если бы они оба шли со скоростью, равной скорости 1-го пешехода, то (t+7/10)(x+x)=42
Получим систему из трех уравнений:
{t(x+y)=42 {tx+ty=42 {tx+ty=42
{(t-1/2)(y+y)=42 <=> {2ty-y=42 <=> {ty=21+0.5y
{(t+7/10)(x+x)=42 {2tx+1.4x=42 {tx=21-0.7x
Сложим второе и третье уравнение:
tx+ty=42+(0.5y-0.7x)
Сопоставляя с первым уравнением системы, очевидно, что 0.5y-0.7x=0. Тогда у=1,4х.
Поставим в первое уравнение:
t(x+1.4x)=42
2.4tx=42
tx=42/2.4=17.5 (км первый пешеход до встречи.
ty=42-17.5=24.5 (км второй пешеход до встречи.
Берем теперь уравнение tx=21-0.7x
17.5=21-0.7x
0.7x=21-17.5
0.7x=3.5
x=5
Значит, 5 км/ч -скорость первого пешехода.
ответ: 5 км/ч.