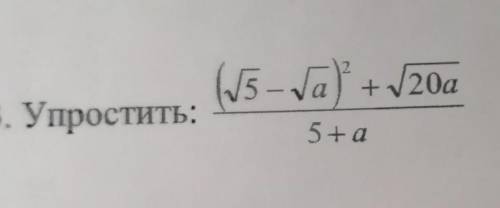
Пошаговое объяснение:
1) 300 = 2 · 2 · 3 · 5 · 5;120 = 2 · 2 · 2 · 3 · 5;100 = 2 · 2 · 5 · 5;НОК (120; 300; 100) = 2 · 2 · 3 · 5 · 5 · 2 = 600;2) 480 = 2 · 2 · 2 · 2 · 2 · 3 · 5; 216 = 2 · 2 · 2 · 3 · 3 · 3;144 = 2 · 2 · 2 · 2 · 3 · 3;НОК (480; 216; 144) = 2 · 2 · 2 · 2 · 2 · 3 · 5 · 3 · 3 = 4320;3) 350 = 2 · 5 · 5 · 7; 105 = 3 · 5 · 7;140 = 2 · 2 · 5 · 7;НОК (105; 350; 140) = 2 · 5 · 5 · 7 · 3 · 2 = 2100;4) 280 = 2 · 2 · 2 · 5 · 7; 140 = 2 · 2 · 5 · 7;224 = 2 · 2 · 2 · 2 · 2 · 7;НОК (280; 140; 224) = 2 · 2 · 2 · 5 · 7 · 2 · 2 = 1120.
Допустим, что такое сложение существует.
Запишем сложение в виде столбика:
М Э Х Э Э Л Э
У Ч У У Т А Л
5 0 5 2 0 2 0
Для удобства пронумеруем разряды: единицы будут 1, десятки -- 2 и так далее до 7.
1. Рассмотрим 1 разряд. "Э + Л = 0".
Это возможно в 2-х случаях:
Э = Л = 0 (не подходит, так как цифры должны быть разные);
Э + Л = 10 (тогда десяток перейдёт на разряд вперёд и останется 0).
Остаётся Э + Л = 10.
2. Рассмотрим 3 разряд. "Э + Т = 0". Возможно три случая:
Э = Т = 0 (не подходит, так как цифры должны быть разные);
Э + Т = 10 (не подходит, так как тогда Т = Л (пункт 1))
Э + Т = 9 (плюс единица из переполнения)
Остаётся Э + Т = 9.
3. Рассмотрим 6 разряд. "Э + Ч = 0". Возможно три случая:
Э = Ч = 0 (не подходит, так как цифры должны быть разные);
Э + Ч = 10 (не подходит, так как тогда Ч = Л (пункт 1))
Э + Ч = 9 (не подходит, так как тогда Ч = Т (пункт 2))
Таким образом, "Э + Ч ≠ 0", а это противоречит условию.
Значит, такого решения быть не может. Что и требовалось доказать.
1
Пошаговое объяснение:
(√5-√а)²+√20а/5+а
раскрыть скобки
5-2√5а+а+√20а/5+а
преобразить части
5+а-2√5а+2√5а/5+а
сократить
5+а/5+а
=1