190 прямых
Пошаговое объяснение:
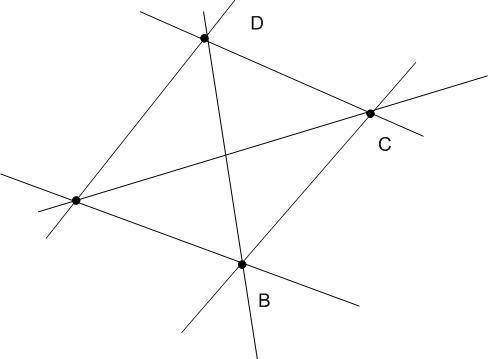
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
Да, сможет. Проверил на 16 клетках. Но передвижения черепашки должен быть, как вроде она двигается по соседним квадратикам змейкой, возвращаясь к тому месту с которого начинала, но не заползать вновь на него, к тому же общее направление движения должно быть параллельно выбранной какой-то стороне до конца доски.
При этом, каждый четвёртый шаг будет обратным(она уже была на этом месте, но цвет после этого поменялся на белый, поэтому нужно вернуться на это место, чтобы он вновь стал чёрным).
Удачи!Здоровья!
Пошаговое объяснение:
Пошаговое объяснение: