Question

Решите уравнение
1) x*5 1/3 =12 3/5 2) x-7 1/8=12 3/5​

Answer 1

Первое уравнение: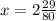 $x=2\frac{29}{80}$, второе: $x=\frac{789}{40}=19\frac{29}{40}$.

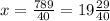Пошаговое объяснение:

Если я правильно понимаю вид уравнений, то первое должно выглядеть так:

$x*5\frac{1}{3}=12\frac{3}{5}$

Для начала нужно перевести дроби в неправильные:

$5\frac{1}{3}=\frac{5*3+1}{3}=\frac{15+1}{3}=\frac{16}{3}$

$12\frac{3}{5}=\frac{12*5+3}{5}=\frac{60+3}{5}=\frac{63}{5}$

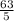Теперь чтобы найти $x$ мы дробь $\frac{63}{5}$ должны разделить на вторую дробь 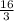$\frac{16}{3}$. Вспоминаем, что при делении дробь на другую дробь, вторая "переворачивается" и происходит умножение двух дробей. Запишем:

$x=\frac{63}{5}:\frac{16}{3}\\\\x=\frac{63}{5}*\frac{3}{16}\\\\x=\frac{189}{80}\\$

Данную дробь, к сожалению, никак не сократить, поэтому можем выделить только её целую часть:

$x=\frac{189}{80}\\\\x=2\frac{189-80-80}{80}\\\\x=2\frac{29}{80}$

Второе уравнение имеет вид:

$x-7\frac{1}{8}=12\frac{3}{5}$

Тут делаем тоже самое, переводим дроби в неправильные:

$7\frac{1}{8}=\frac{7*8+1}{8}=\frac{56+1}{8}=\frac{57}{8}$

$12\frac{3}{5}=\frac{12*5+3}{5}=\frac{60+3}{5}=\frac{63}{5}$

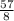Но теперь, чтобы найти $x$ требуется дробь $\frac{57}{8}$ перенести в правую часть уравнения, и дробь 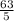$\frac{63}{5}$ сложить с данной дробью:

$x=\frac{63}{5}+\frac{57}{8}$

Нам требуется привести две дроби к общему знаменателю, который находится путем перемножения знаменателей. Общий знаменатель будет равен: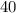 $40$.

Домножаем первую дробь на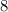 $8$, а вторую на 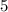$5$, получаем:

$x=\frac{63}{5}+\frac{57}{8}\\\\x=\frac{63*8+57*5}{5*8}\\\\x=\frac{504+285}{40}\\\\x=\frac{789}{40}$

Данная дробь также не сокращается, просто выделяем ее целую часть:

$x=\frac{749}{40}\\\\x=19\frac{749-40*19}{40}=19\frac{29}{40}$