Нельзя.
Пошаговое объяснение:
1) Понятно, что нельзя ставить простые числа, большие 15, т.к. они взаимно просты с любым из ост. чисел.
2) Также нельзя ставить единицу, т.к. не имеет делителей больше единицы.
3) Наконец, 11 и 13 нельзя ставить, т.к. имеют только 1 делитель, в то время как имеют хотя бы 2 общие стороны с другими числами.
4) Тогда, мы можем ставить 30(чисел) - 4(простых числа > 15: 17, 19, 23, 29 ) - 1(единица) - 2(11 и 13) = 23 числа.
5) Т.к. в таблице 24 места, нельзя использовать одинаковые числа и всего чисел, которые можно поставить - 23, то ответ - нельзя.
566300 : 70 = 56630 : 7 = 8090.
Пошаговое объяснение:
Если делимое 566300 и делитель 70 разделить на одно и то же число 10, то значение частного не изменится.
Именно поэтому у двух данных чисел можно отбросить по одному нулю в конце записи чисел.
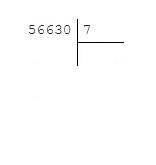
566300 : 70 = 56630 : 7
Записываем эти числа в столбик (рис. 1)
Правило
1. Выделяем первое неполное делимое 56. Определяем количество цифр в значении частного. Их будет 4.
2. Подбираем первую цифру в значении частного. 56 : 7 = 8.
3. Умножаю число, записанное этой цифрой, на делитель. 7·8 = 56.
4. Вычитаем полученный результат из неполного делимого и находим остаток: 56 - 56 = 0. Остатка нет. (рис. 2)
5. Записываем цифру следующего разряда делимого рядом с остатком. Получаем второе неполное делимое 6. 6 на 7 не делится, записываю в частное 0, (рис. 3), приписываю ещё одну цифру 3.
6. Делю число 63 на 7. Получаю 9. (рис. 4)
63 - 63 = 0.
7. Последний нуль записываю в частное. (рис. 5)
Деление выполнено.
566300 : 70 = 56630 : 7 = 8090.
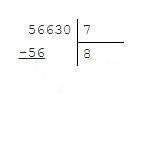
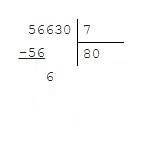
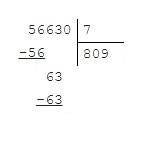

х + 4/15 = 2/3 + 2/5
х = 2/3 + 2/5 - 4/15
х = (10 + 6 - 4)/15
х = 12/15
х = 4/5
б)
(4/5 - х) + 13/20 = 25/30
4/5 - х + 13/20 = 25/30
-х = 25/30 - 4/5 - 13/20
-х = (50 - 48 - 39)/60
-х = -37/60
х = 37/60
в)
у - 5/20 = 5/8 - 3/10
у = 5/8 - 3/10 + 5/20
у = (25 - 12 + 10)/40
у = 23/40
г)
2/3 - ( 7/9 - а) = 1/3
2/3 - 7/9 + а = 1/3
а = 1/3 - 2/3 + 7/9
а = (3 - 6 + 7)/9
а = 4/9