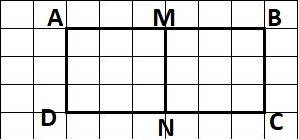
Начертим прямоугольник ABCD, стороны которого равны 3 см и 1 см 5 мм (2 клетки равняются 1 см):
AB=DC=3 см; AD=BC=1 см 5 мм
Проведя отрезок MN, такой, что M∈AB, N∈DC, мы разделим прямоугольник ABCD на два одинаковых квадрата - AMND и MBCN.
Длина квадратов будет в два раза меньше, чем длина прямоугольника, т.е. 3:2=1 см 5 мм; ширина такая же, как и у прямоугольника.
1 см=10 мм ⇔ 3 см=30 мм, 1 см 5 мм=15 мм
Периметр равен сумме длин всех сторон:
1) P=30+30+15+15=2*(30+15)=2*45=90 (мм) - периметр прямоугольника.
2) P=15+15+15+15=4*15=60 (мм) - периметр каждого квадрата.
Чертеж во вложении.
Существует правило: a (b + c) = ab + ac.
Таким образом, умножаешь множитель перед скобкой на каждый член в скобках.
Если можно разложить по формуле (как в третьем примере (7 - с)²) - раскладывай.
В конце сокращай подобные члены (например, если у тебя есть 5а + 8а + 13с, то это можно представить как 13а + 13с)
3a (2b - 5) + 3m (5 - 2b) = 6ab - 15a + 15m - 6bm
- (a + 3b) - 5 (a + 3b)² = - a - 3b - 5 (a² + 6аb + 9b²) = - a - 3b - 5a² - 30аb - 45b² = - а - 3b - 5a² - 30ab - 45b²
(с - 7)х - у(7 - с)² = сх - 7х - у (49 - 14с + с²) = сх - 7х - 49у + 14су - с²у