
9216
Пошаговое объяснение:
Предположим, что существует несократимая дробь, наибольший общий делитель d числителя и знаменателя которой отличен от 1. Но тогда эту дробь можно сократить на d. Получили противоречие, а значит, числитель и знаменатель являются взаимно простыми. Поскольку у правильной дроби числитель меньше знаменателя, то для ответа на вопрос необходимо вычислить количество чисел, взаимно простых с 8! и не превышающих 8! Задача сводится к нахождению функции Эйлера φ от числа 8!
Воспользуемся свойством мультипликативности функции Эйлера:
если a и b — взаимно простые, то φ(ab) = φ(a)φ(b)
Замечу, что степени двух различных простых чисел (p_1)^α и (p_2)^β являются еще и взаимно простыми:
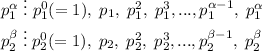
(видно, что у (p_1)^α и (p_2)^β нет общих делителей, кроме 1)
Исходя из изложенного, если записать каноническое разложение 8! на простые множители:
8! = 8×7×6×5×4×3×2×1 = 2³×7×2×3×5×2²×3×2 = 2^7 × 3² × 5 × 7,
то станет целесообразно упростить решение: φ(8!) = φ(2^7)φ(3²)φ(5)φ(7)
А теперь приведу формулу для вычисления φ(p^α) (p — простое):
φ(p^α) = p^α - p^(α-1)
Если же α = 1, то:
φ(p) = p-1
Имеем:
φ(8!) = φ(2^7 × 3² × 5 × 7) = φ(2^7)φ(3²)φ(5)φ(7) = (2^7 - 2^6)(3² - 3)(5-1)(7-1) = 2^6(2-1) × 3(3-1) × 4 × 6 = 64×3×2×4×6 = 9216,
что и есть ответ на вопрос задачи.
2) 250-108=142 км осталось проехать
3) 4-2=2 ч осталось ехать, что путь занял 4 ч
4) 142:2=71 км/ч должна быть скорость автомобиля
5) 71-54=17 км/ч надо увеличить скорость
ответ В на 17 км/ч
№4
Размещаем цифры от 1-9 в квадрате следующим образом:
1 2 9
4 3 8
5 6 7
Сумма диагонали:
1 + 3 + 7 = 11
ответ В 11
№5 Дополним условие. Оля задумала натуральное число меньше 30 и нашла его остатки от деления на 6 и на 9. Сумма этих остатков оказалась равна 13. Найдите остаток от деления этого числа на 18
Остаток от деления на 6 может быть от 0 до 5, на 9 от 0 до 8.
Сумму остатков от деления 13 можно получить:
5+8=13 - только 1 вариант
Значит это число можно найти как:
9+8=17
6*2+5=17
При условии что это число меньше 30 только 1 вариант 17.
17:18=0 (ост. 17)
ответ Г) 17