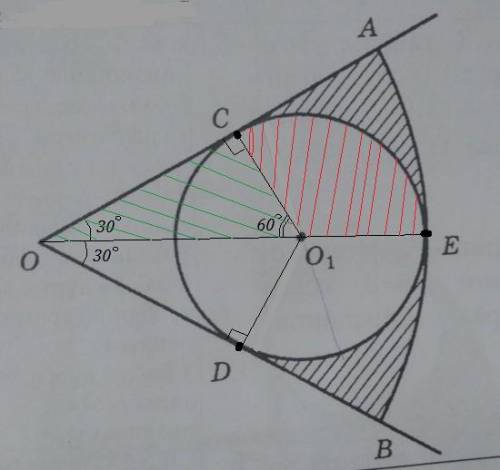
Соединим точки О и О₁ , ОО₁ - биссектриса , так как на биссектрисе лежит центр вписанной окружности ⇒ ∠СОО₁ =60°
Рассм. ΔСОО₁ . Точка С - точка касания ⇒ ∠О₁СО=90° , СО₁=а , Катет, лежащий против угла в 30°, равен половине гипотенузы, значит ОО₁=2*СО₁=2а .
Если продолжить ОО₁ далее, то точка касания Е - будет лежать на биссектрисе ОО₁ , и ОЕ=ОО₁+О₁Е=2а+а=3а .
Площадь сектора АОЕ равна
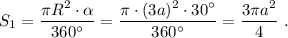
Площадь четверти круга СО₁Е радиуса "а" равна
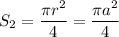 .
.
Площадь ΔОО₁С равна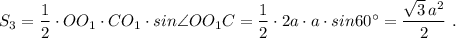
Площадь искомой фигуры в силу симметрии равна
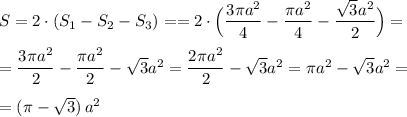
53 + 18 = ( 50 + 3) + ( 10 + 8) = ( 50 + 10) + ( 3 + 8) = 60 + 11 = 71
53 + 28 = ( 50 + 3) + ( 20 + 8) = ( 50 + 20) + ( 3 + 8) = 70 + 11 = 81
53 + 38 = ( 50 + 3) + ( 30 + 8) = ( 50 + 30) + ( 3 + 8) = 80 + 11 = 91
вычислив первый пример, можем заметить, что в каждом следующем, второе слагаемое на десяток больше, не вычисляя можно написать ответы))
73 + 17 = ( 70 + 3) + ( 10 + 7) = (70 + 10) + ( 3 + 7) = 80 + 10 = 90
73 + 19 = ( 70 + 3) + ( 10 + 9) = ( 70 + 10) + ( 3 + 9) = 80 + 12 = 92
73 + 18 = ( 70 + 3) + ( 10 + 8) = ( 70 + 10) + ( 3 + 8) = 80 + 11 = 91
55 + 29 = ( 50 + 5) + ( 20 + 9) = ( 50 + 20) + ( 5 + 9) = 70 + 14 = 84
46 + 38 = ( 40 + 6) + ( 30 + 8) = ( 40 + 30) + (6 + 8) = 70 + 14 = 84
37 + 47 = ( 30 + 7) + ( 40 + 7) = ( 30 + 40) + ( 7 + 7) = 70 + 14 = 84
т.е. 35% это 21 страница
тогда 0,35х = 21
х = 21 : 0,35
х = 60 страниц всего было в книге