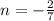 - знаменатель обращается в 0.
- знаменатель обращается в 0.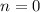 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)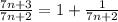

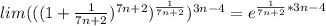 (при
(при  →∞)
→∞)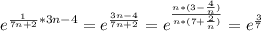 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→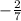
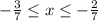 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
Перпендикуляром, проведеним з деякої точки до заданої прямої, називається відрізок, що лежить на прямій, перпендикулярній до заданої прямої і з кінцями в заданій точці, і точки, що лежить на заданій прямій. Кінець перпендикуляра, що лежить на прямій, до якої він проведений, називається основою перпендикуляра.
Похила — будь-який відрізок, проведений із точки на пряму, відмінний від перпендикуляра. Кінець похилої, що лежить на прямій, до якої він проведений, називається основою похилої.
Відрізок, що сполучає кінець перпендикуляра і похилої до прямої, проведених з однієї точки, називається проекцією похилої на пряму.
Якщо до прямої з однієї точки проведені перпендикуляр і похилі, то будь-яка похила більша від перпендикуляра.
Рівні похилі мають рівні проекції.
Якщо проекції похилих рівні, то рівні і похилі.
Із двох похилих більшою є та, у якої більша проекція на пряму.
Більшій похилій відповідає більша проекція і навпаки.
Термы-античные бани в классической Греции — при больших домах и гимнасиях; в период эллинизма ими пользовалось всё население города. В Древнем Риме термы возникли по греческому образцу и стали центрами общественной жизни.Первые термы выстроил в Риме Агриппа .Внутри императорские термы были выполнены из мрамора, украшены мозаикой, скульптурами и мраморными колоннами, окна и двери были из бронзы. В термах находились следующие помещения: одежду оставляли в раздевалке, затем посетитель мог заняться спортом или смазать тело маслами. Банная «программа» начиналась с купания в холодной воде затем в чуть теплой воде и потом с теплой водой.Римские архитекторы разработали эффективную систему центрального отопления с подогревом пола и стен — гипокауст. В термах с печи нагревались вода и воздух, которые затем циркулировали под полом и в полостях стен. При этом использовались двойные покрытия, чтобы пол не был очень горячим. Верхнее покрытие состояло из больших кирпичей, слоя битой глины и основного покрытия. Все это держалось на небольших кирпичных опорах (pilae), которые сразу размещали в шахматном порядке. В стены были встроены прямоугольные кирпичи, внутри Древнеримские термы строились по всей территории Римской империи, но до наших дней сохранились, как правило, только в виде руин. Лучше всего сохранились термы Каракаллы , которые уже в 5 веке н. э. считались одним из чудес Рима.Они крепились металлическими скобами. Внутри стены терм были украшены мрамором или оштукатурены.