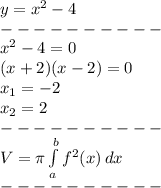
![V= \pi \int\limits^2_{-2} {(x^2 -4)^2} \, dx =\pi \int\limits^2_{-2} {(x^4 -8x^2+16)} \, dx = \\ \\ =\pi ( \frac{x^5}{5} -8* \frac{x^3}{3}+16x)|^2_{-2} = \\ \\ =\pi [( \frac{2^5}{5} -8* \frac{2^3}{3}+16*2)-(\frac{(-2)^5}{5} -8* \frac{(-2)^3}{3}+16*(-2))]= \\ \\ = \pi [( \frac{32}{5} -8* \frac{8}{3}+32)-(\frac{-32}{5} -8* \frac{-8}{3}-32)]= \\ \\ = \pi [( \frac{32}{5} -\frac{64}{3}+32)-(\frac{-32}{5} + \frac{64}{3}-32)]=](/tpl/images/0279/7377/a7de5.png)
![= \pi [( \frac{32}{5} -\frac{64}{3}+32+\frac{32}{5} - \frac{64}{3}+32)]= \\ \\ = \pi [( \frac{64}{5} -\frac{128}{3}+64)]= \\ \\ = \pi ( \frac{64*3-128*5+64*15}{15})= \\ \\ = \pi ( \frac{192-640+960}{15})= \\ \\ = \frac{512*\pi}{15}=107,233](/tpl/images/0279/7377/b6fb5.png)
Правильная четырехугольная пирамида 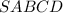 .
.
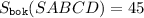 (см²).
(см²).
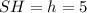 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
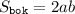 , где
, где  - сторона основания и
- сторона основания и 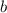 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 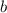 через
через  (сторону основания) и
(сторону основания) и 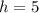 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 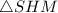 (где
(где 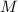 - середина
- середина 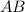 ). В нем
). В нем 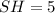 (см), а
(см), а 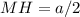 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
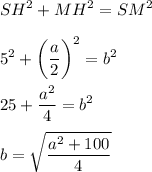
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
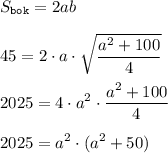
Пусть 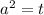 :
:
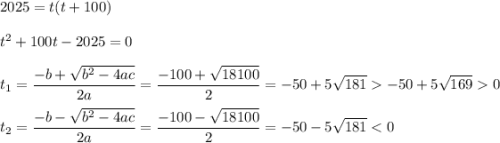
Второй корень нам не подходит по причине отрицательности. Значит:
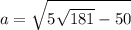
Задача решена!
ответ: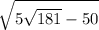 или около
или около 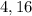 (см).
(см). 