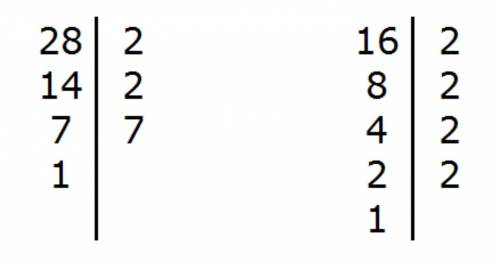
1 и 2) Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются - простыми числами. Числа, имеющие другие делители, называются составными числами.
3) Из вышесказанного следует, что единицу нельзя назвать ни простым, ни составным числом, так как простое имеет 2 делителя, а единица только один.
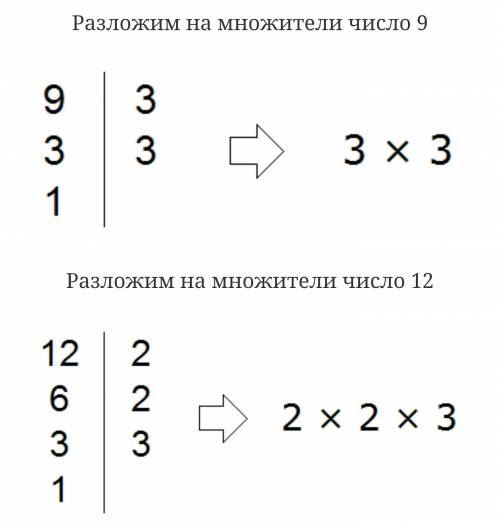
4) Подозреваю, что тут имеют ввиду при каких случаях получается число 24.
К примеру: 24= 2*4*3 (таких примеров довольно много).
5) Это наибольший из общих делителей.
6) Числа взаимно простые, если они не имеют никаких общих делителей, кроме ±1.
7) а) Разложить на простые множители;
б) Из этих множителей, которые входят в разложение одного из этих чисел, убрать те, которые не входятв разложении другого числа;
в) Найти произведение оставшихся чисел .
8) Наим.общ.кратное - наименьшее натуральное число, которо кратно и а и б.
9) Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Главной идеей научного творчества Галилея было представление о мире как упорядоченной системе тел, которые движутся одно относительно другого в однородном пространстве, лишенном привилегированных направлений или точек. Например, что считать верхом или низом, по Галилею зависит от выбранной системы отсчета. В аристотелевской же физике мир представлял собой ограниченное, пространство, где верх или низ четко различались. Все тела либо покоились в своих «естественных местах», либо двигались по направлению к ним. Однородность пространства, относительность движения – таковы были принципы новой научной картины мира, заложенные Галилеем. Кроме того, у Аристотеля покой был важнее и лучше движения: у него тело, на которое не действовали силы, всегда находится в покое. Галилей же ввел принцип инерции (если на тело не действуют силы, оно покоится либо равномерно движется), который уравнял покой и движение. Теперь движение с постоянной скоростью не требует причины. Это был величайший переворот в учении о движении, положивший начало новой науке. Вопрос о конечности или бесконечности мира Галилей считал неразрешимым.
ГАЛИЛЕЙ ВПЕРВЫЕ СОЕДИНИЛ ФИЗИКУ С МАТЕМАТИКОЙ
Важнейшей новацией Галилея в науке было его стремление математизировать физику, описывать окружающий мир не на языке качеств, как в аристотелевской физике, а на языке математики. Галилей писал: «Никогда я не стану от внешних тел требовать чего-нибудь иного, чем величина, фигура, количество и более или менее быстрые движения для того, чтобы объяснить возникновение ощущений вкуса, запаха и звука. Я думаю, что если бы мы устранили уши, языки, носы, то остались бы только фигуры, числа, движения, но не запахи, вкусы и звуки, которые, по моему мнению вне живого существа являются не чем иным, как только пустым мнением». И когда знаменитый физик, лауреат Нобелевской премии по физике 1979 года Стивен Вайнберг говорит, что суть современной физики – количественное понимание явлений, важно знать, что основу этого заложил Галилео Галилей в своих экспериментах по измерению движения падающих с вершины башни камней, качения шаров по наклонной плоскости и т.д.