ответ:
распределительное. распределительное свойство применяется только относительно сложения. распределительное свойство гласит: если число умножается на сумму, то можно каждое из слагаемых умножить на это число, а результаты сложить.
сочетательное.
сочетательное свойство говорит о том, что при перемножении трех и более чисел, можно перемножить два первых числа, а результат использовать дальше в качестве множителя. то есть 3*4*5=12*5=60
переместительное. переместительное свойство гласит, от перемены мест множителей произведение не меняется.
распределительное свойство может применяться и относительно вычитания или деления. с этого свойства раскрывают скобки в примерах при необходимости.
переместительное свойство
правильное использование определения переместительного свойства умножения может увеличить скорость счета. к сожалению, специальных правил группировки нет. нужно полагаться только на собственный опыт и логику. рассмотрим небольшой пример, чтобы показать применение свойства на практике:
((15*25*7*3: 125)-3): 12 – в этом примере можно только правильно сгруппировав произведение в скобках для ускорения деления. для этого представим число 15 в виде произведения 3*5
((15*25*7*3: 125)-3): 12=((5*3*25*7*3: 125)-3): 12 теперь перемножим 5 и 25, выполним деление произведения на число. для этого можно только один из множителей разделить на это число, а потом результат использовать, как один из множителей.
*25)*3*7*3: 125)-3): 12=((125*3*7*3: 125)-3): 12=(3*3*7-3): 12=(9*7-3): 12=(63-3): 12=60: 12=5
без переместительного свойства не удалось бы правильно сгруппировать множители, а значит пришлось бы считать пример полностью, что отняло бы большое количество времени
ответ Замятина - "силой Разума" на рисунках в приложении.
Всё решение начинается от ТОЧКИ.
Одна точка А - ничтожная малость, но ведь такиех точек бесконечно много и из них можно построить множество фигур разной формы.
У плоских многоугольников -стороны фигуры являются отрезками прямых линий - у треугольника их три, а у квадрата - четыре.
Простейшая плоская фигура, но совсем без углов - это круг.Так и хочется назвать: круг - безугольник, а шар (сфера) - безгранник. Сфера, круг, как и квадрат "идеальные" фигуры - минимальный объём, минимальный периметр.
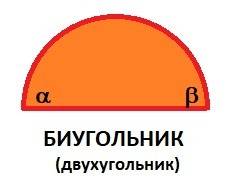
Попробуем превратить часть круга в отрезок прямой - положить его на прямую и .... получим биугольник - фигуру с двумя углами - рисунок в приложении.
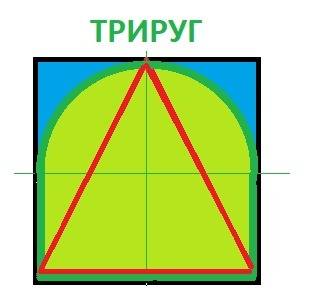
Дальнейшие рассуждения приводят к нам к фигуре которая состоит из трёх отрезков и части круга. Получилась фигура и не треугольник и не квадрат. Назовём, например, трируг.
Всё это решение, конечно, фантазия на тему как одна фигура превращается в другую. А всё это начинается обычной, бесконечно-малой математической точки А.
15-10=5 ст разница между 1 и 2 залом
20:5=4 места за 1 столом
15*4=60 мест в 1 зале
10*4=40 мест во 2 зале