Формула, устанавливающая зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то S₁ = 7,2 (см²)
2) если h = 2, то S₂ = 7,2h = 14,4 (см²)
1) если h = 3,6, то S₃ = 7,2h = 25,92 (см²)
Пошаговое объяснение:
Требуется записать формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h. Пользуясь формулой, вычисли S, если h = 1; 2; 3,6.
Площадь боковой поверхности параллелепипеда найдем по формуле:
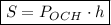 , где Р - периметр основания, h - высота.
, где Р - периметр основания, h - высота.
По условию Росн. = 7,2 см.
Составим формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то
S₁ = 7,2h = 7,2 · 1 = 7,2 (см²)
2) если h = 2, то
S₂ = 7,2h = 7,2 · 2 = 14,4 (см²)
1) если h = 3,6, то
S₃ = 7,2h = 7,2 · 3,6 = 25,92 (см²)
F'(x)=1-6/x^3
Находим точки экстремума:
1-6/х^3=0
1=6/x^3
x^3=6
и х не равен 0
x^3-6=0
(x-куб.кор(6))*(x^2+куб.кор(6)*x+куб.кор(36)
последний множитель корней не имеет
следовательно только одна точка эстремума :
x=куб.кор(6) и она пренадлежит заявленному промежутку.