1 уравнение X = 10 2 уравнение X = 7
Пошаговое объяснение:
13 + 6 - X = 9 5 + 8 + X = 20
19 - X = 9 13 + X = 20
- X = - 10 X = 7
X = 10
19 - X = 9, мы переносим 19 в правую часть уравнения, поэтому идет с противоположным знаком - 19 + 9 = - 10, а X не бывает с минусом, поэтому переносим минус в правую часть уравнения и получается -(-10) = 10
Аналогично и с 13 + X = 20, мы также переносим 13 в правую часть уравнения(неизвестные в левую часть - X, а известные в правую часть) и получаем 7
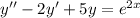
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является 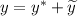 .
.
1) 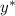 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
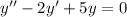
Применим метод Эйлера: сделаем замену 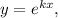 где
где 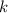 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 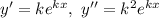
Получили характеристическое уравнение:
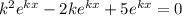
Разделим обе части уравнения на 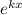 :
:
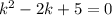
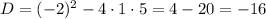
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
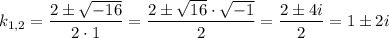
Тогда 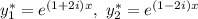
Воспользуемся формулой Эйлера: 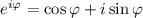
Фундаментальная система решений: 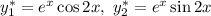 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 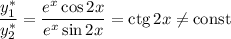
Общее решение: 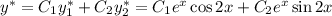
2) 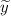 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 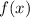 .
.
Здесь 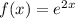 , причем
, причем 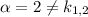 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 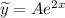 , где
, где 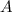 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда 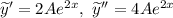 и
и 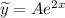 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 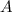 :
:
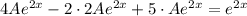
Разделим обе части уравнения на 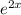
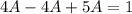
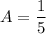
Таким образом, частное решение: 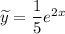
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
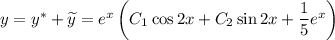
ответ: 
2)(2396+814)-(36×9)=2886