Область определения запишем
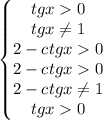
Систематизируем немного
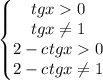
Из последнего видим, что 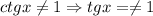 , а это уже есть. Остается тогда
, а это уже есть. Остается тогда
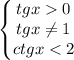
Правда, решая неравенство 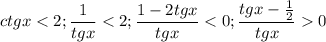
методом интервалов, получаем
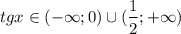
Но тангенс из другого неравенства больше нуля, поэтому
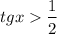 и не забываем
и не забываем 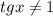 , вот все ограничения.
, вот все ограничения.
Теперь решаем неравенство:
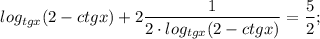
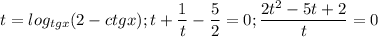
Тут t явно не равно нулю в числителе, поэтому это ограничение нам особо не нужно.

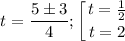
Решаем 1-ое уравнение (t=1/2):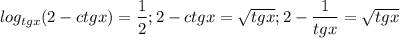
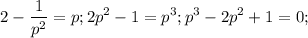
Видно по сумме коэффициентов, равно 0, что p=1 - корень уравнения. Однако, 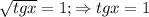 , но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
, но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
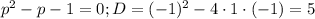
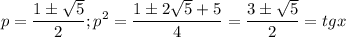
Видно, что оба значения положительны, но второе и больше 1/2, так как в числителе число, куда больше, чем 1.
А вот другой корень проверим:
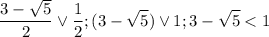 , а значит, tgx <1/2 в этом случае и это нам не подходит, отсюда берем лишь
, а значит, tgx <1/2 в этом случае и это нам не подходит, отсюда берем лишь
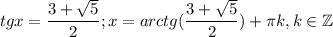
Решаем второе уравнение:
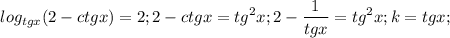
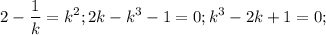
(то, что 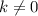 здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
Тут сумма коэффициентов равна 0, k=1 - корень. Поделим на k-1 уголком или по схеме Горнера и получим
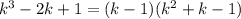
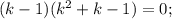
Корень k=1=tgx нам не подходит, так как по ограничениям 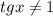
Решаем квадратное уравнение, которое дает нам вторая скобка.
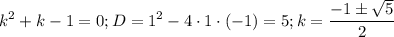
Отрицательный корень не берем, так как 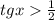
Проверим положительный корень на выполнение ограничений (сравня с 1/2)
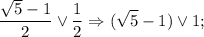
Левое выражение больше правого, значит, этот корень удовлетворяет 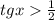 (так как
(так как 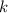 это не целое число, то оно не равно 1, то есть
это не целое число, то оно не равно 1, то есть 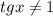 , поэтому корень подходит)
, поэтому корень подходит)

ответ: 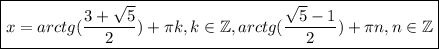
ответ:В отряде 7 офицеров и 20 рядовых. Сколькими можно сформировать разведывательную группу из 3 офицеров и 12 рядовых?
Пошаговое объяснение:
Трех офицеров из 10 можно выбрать С где С(10,3) - число сочетаний из 10 по 3.
С(10,3) = 10! / (3! · (10 - 3)!) = 10! / (3! · 7!) =
= 8 · 9 · 10 / (1 · 2 · 3) = 120;
Семь солдат из 20 можно выбрать С С(20,7) = 20! / (7! · (20 - 7)!) = 20! / (7! · 13!) =
= 14 · 15 · 16 · 17 · 18 · 19 · 20 / (1 · 2 · 3 · 4 · 5 · 6 · 7) = 77520;
Всего выбрать разведывательную группу:
С(10,3) · С(20,7) = 120 · 77520 = 9302400.
ответ: 9302400.
12070+9500=21570(кг) или 21т 570 кг