Задача. Привести к общему знаменателю дроби
\frac{5}{10}, \frac{5}{12}.
10
5
,
12
5
.
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. НОК(10, 12) = 60. Это число и будет новым знаменателем.
Чтобы знаменатели дробей стали равны 60, надо:
Числитель и знаменатель 1-й дроби домножить на 6 = 60 : 10. Получаем:
\frac{5}{10} = \frac{5 \,\cdot\, 6}{10 \,\cdot\, 6} = \frac{30}{60}
10
5
=
10⋅6
5⋅6
=
60
30
Числитель и знаменатель 2-й дроби домножить на 5 = 60 : 12. Получаем:
\frac{5}{12} = \frac{5 \,\cdot\, 5}{12 \,\cdot\, 5} = \frac{25}{60}
12
5
=
12⋅5
5⋅5
=
60
25
ответ: \frac{30}{60}, \frac{25}{60}
60
30
,
60
25
Пошаговое объяснение:
а) -20 = -5 + (-15);
б) -20 = -14,6 + (-5,4);
в) 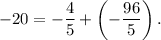
Объяснение:
Требуется представить число (-20) в виде суммы двух отрицательных слагаемых, учитывая заданные условия.
Вспомним правило сложения чисел одного знака:
чтобы сложить два числа одинаковых знаков, нужно сложить их модули и поставить перед суммой знак слагаемых.
а) Оба слагаемых целые числа.
Представим число (-20) в виде суммы двух целых отрицательных чисел, например, так:
-5 + (-15) = -(5+15) = -20.
б) Оба слагаемых десятичные дроби.
Представим число (-20) в виде суммы двух отрицательных десятичных дробей, например, так:
-14,6 + (-5,4) = -(14,6 + 5,4) = -20.
б) Одно из слагаемых правильная дробь.
Положительная дробь называется правильной, если ее числитель меньше знаменателя. Если перед положительной дробью поставить знак минус, то получится отрицательная дробь.
Например, так представим число (-20) в виде суммы двух отрицательных дробей, одна из которых правильная.
Число (-20) представим в виде дроби со знаменателем 5, а потом полученную дробь представим как сумму двух дробей (не забудем, что одна из них должна быть правильной):
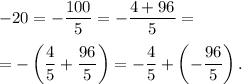
2) 4+4 = 8 частей картин всего
3) 280:8=35 картин - в одной части = кол-во натюрмортов
4) 35*3=105 картин - в трёх частях = кол-во пейзажей
5) 35+105=140 картин - портретов