21π+9√2π см²
Пошаговое объяснение:
1)
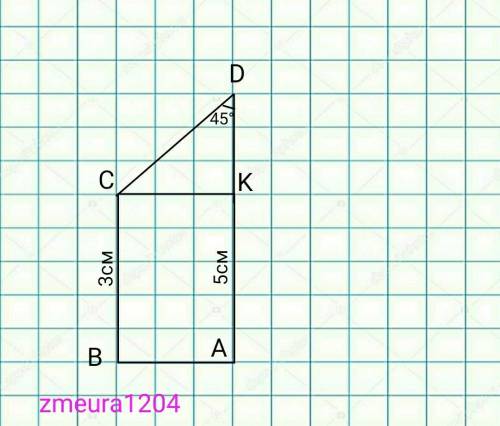
АК=ВС=2см
КD=AD-AK=5-2=3см
∆СКD- прямоугольный равнобедренный треугольник.
(<СКD=90°; <KDC=45°; <DCK=180°-90°-45°=45°) углы при основании равны.
КD=CK=3см.
Теорема Пифагора
СD=√(CK²+KD²)=√(3²+3²)=3√2 см
ВА=СК=3см.
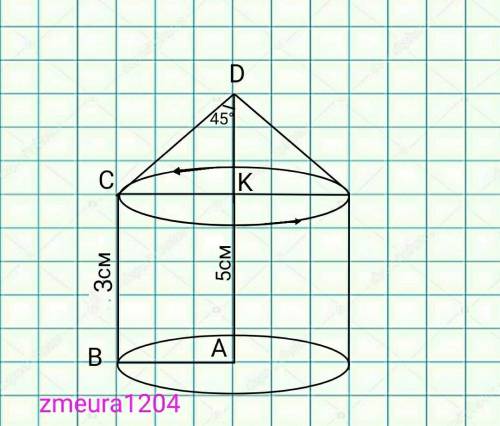
При вращении получили конус и цилиндр.
СК=R=3см
Sбок.к=πRL=π*CK*CD=π*3*3√2=9√2π см² боковая площадь конуса
Sбок.ц.=2πR*h=2π*BA*BC=2π*3*2=12π см² площадь боковой поверхности цилиндра.
Sосн.ц.=πR²=π*AB²=π*3²=9π см²
Sз.ф.=Sбок.к+Sбок.ц.+Sосн.ц=
=9√2π+12π+9π=21π+9√2π см²
16π+4√2 см²
Пошаговое объяснение:
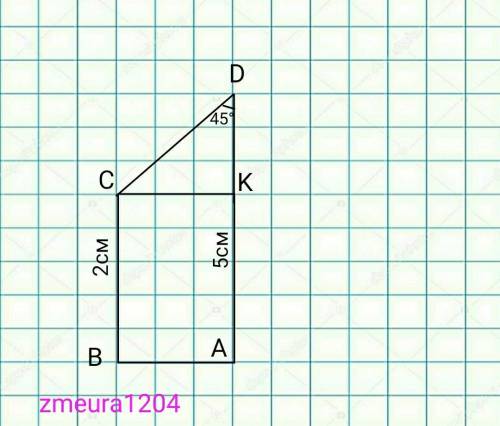
CB=AK=3см
КD=AD-AK=5-3=2см
∆СKD- прямоугольный равнобедренный треугольник
(<СКD=90°; <CDK=45°; <DCK=45°) углы при основании равны. СК=KD=2см
По теореме Пифагора
СD=√(CK²+KD²)=√(2²+2²)=2√2 см
СК=ВА=2см.
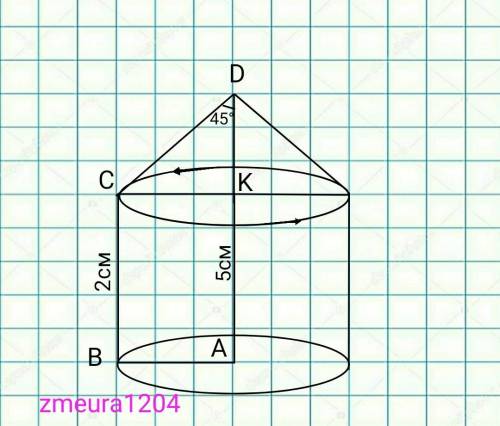
При вращении получили конус и цилиндр с равным радиусом
R=CK=BA=2см
Sбок.к.=πRL=π*CK*CD=π*2*2√2=4√2π см² площадь боковой поверхности конуса
Sбок.ц=2πRh=2π*BA*BC=2π*2*3=12π см² площадь боковой поверхности цилиндра.
Sосн.ц=πR²=π*2²=4π см² площадь основания цилиндра.
Sз.ф.=Sбок.к+Sбок.ц+Sосн.ц=
=4√2π+12π+4π=16π+4√2π см² площадь заданной фигуры.