Для начала нужно построить координатную плоскость ху.
Вершины имеют определенные координаты, которые надо отметить на построенной плоскости (я брала 1 клетку за 1 см).
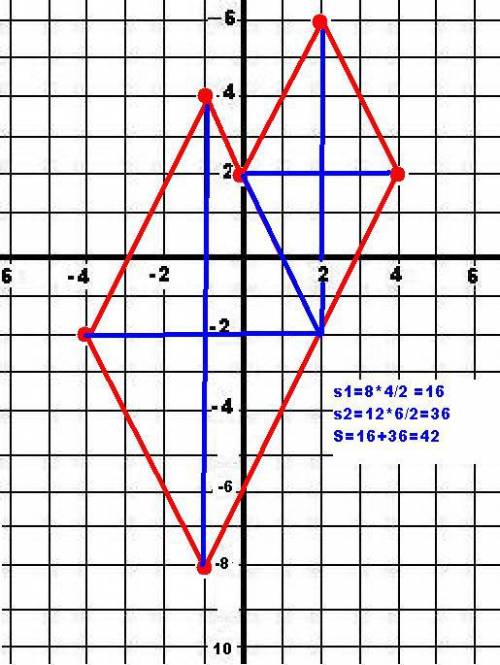
По рисунку видно, что полученная фигура похожа на 2 ромба.
Для того, чтобы посчитать площадь этой фигуры мы используем формулу площади ромба S = 1/2 d1d2, где d1 и d2 – диагонали ромба.
Эти диагонали мы можем узнать из получившегося рисунка (просто измерить линейкой расстояние).
Отметим точку L.
Рассмотрим ромб BAFL.
BF=12см, LA=6см.
Следовательно S BAFL = 1/2*(12*6) = 36см.
Аналогично с ромбом CLED
LD=8 см, CE= 4 см.
S CLED= 1/2*(8*4) = 16 см.
1) 2^8+4^5-8^2=2^8+(2^2)^5-(2^3)^2=2^8+2^10-2^6=2^6*(2^2+2^4-1)=2^6*(4+16-1)=2^6*19=2^5*(2*19)=2^5*38 это выражение делится на 38
(2^5*38)/38=2^5=32 что требовалось доказать
2) 3^11+9^6+27^3=3^11+(3^2)^6+(3^3)^3=3^11+3^12+3^9=3^9*(3^2+3^3+1)=3^9*(9+27+1)=3^9*37=3^8*(3*37)=3^8*111 это выражение делится на 111
(3^8*111)/111=3^8 что требовалось доказать
3) a=9^7+9^6+9^5=(3^2)^7+(3^2)^6+(3^2)^5=3^14+3^12+3^10=3^10*(3^4+3^2+1)=3^10*(81+9+1)=3^10*91.
b=3^10-3^9+3^8=3^8*(3^2-3+1)=3^8*(9-3+1)=3^8*7
(3^10*91)/(3^8*7)=3^2*91/7=9*13=117 что и требовалось доказать а делится на b2/3-(5/6-x)=1/12 5/6-x=2/3-1/12 5/6-x=7/12 x=5/6-7/12 x=1/4 проверка 2.3-(5/6-1/4)=1/12
Дополним еще одну линию и получается два ромба.