Ну и задачка)
Число A имеет вид
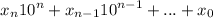
Число B (число А после перестановки) имеет вид
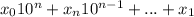
2А=B
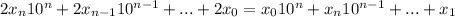
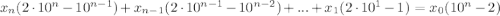

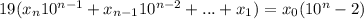
Далее анализируем. Выражение справа должно делиться на 19. Но так как 19 - простое число, а все коэффициенты 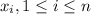 являются цифрами, то есть натуральными числами с 1 по 9, то x0 не разделится на 19 никак, а значит,
являются цифрами, то есть натуральными числами с 1 по 9, то x0 не разделится на 19 никак, а значит, 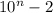 делится на 19.
делится на 19.
Признак делимости на 19 есть, конечно: число без последней цифры + удвоенная последняя цифра ( их сумма имеется в виду) должна делиться на 19. Можно применять последовательно. Но я как-то не вижу возможности в общем виде это расписать. 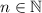 , естественно. В общем, мучаясь и страдая, подбором получаем
, естественно. В общем, мучаясь и страдая, подбором получаем
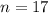
И поделив на 19 число 99999999999999998, получаем 5263157894736842. Но что это? Если посмотрим на выражение
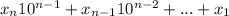
то станет ясно, что это записанное число до перестановки без последней цифры
а выражение справа получается
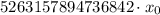
Теперь надо подобрать натуральное решение этого уравнения.
Анализируем возможные 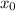
1 быть не может, так как получится это же число, к нему в конец должна добавиться 1 (х0) но там спереди 5, а на будет конце 1, а при переставлении число должно удвоиться, а так как разрядность чисел одинакова, то старший коэффициент должен тоже минимум удвоиться, а здесь такого нет.
А вот что будет при 2:
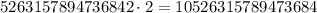
Удивительно, но при добавлении 2 в конце, которая потом пойдет вперед число вполне себе удваивается. Проверим
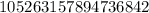
Переставив 2 в начало, получим 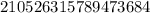
Ну и поделив второе на первое, получим
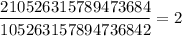
Работает. Удивительно, что Вере это число показалось малым))
ответ: 
Я думаю що це буде так