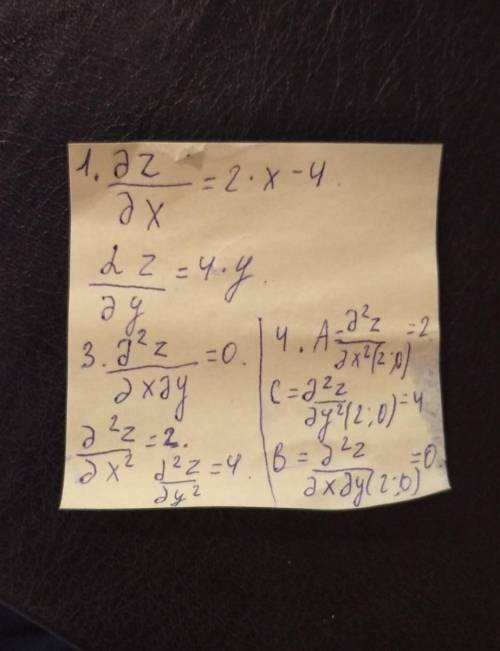Пошаговое объяснение:
а) число всех равновозможных случаев, одно из которых обязательно произойдет при бросании монеты равно 2, так как монета имеет две стороны;
количество случаев, благоприятствующих выпадению герба равно 1, так как герб расположен только на одной стороне монеты;
вероятность выпадения герба при однократном бросании монеты равна 1/2
Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при двух бросках монеты.
Вероятность не выпадения герба при однократном бросании монеты равна 1/2
вероятность не выпадения герба при втором броске монеты так же равна 1/2
вероятность не выпадения герба при двух бросках монеты равна
1/2 * 1/2 = 1/4
, тогда 1 − 1/4 = 3/4
вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты.
б)по аналогии с подпунктом а) Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при трёх бросках монеты.
Вероятность не выпадения герба при трёх бросках монеты равна
1/2 * 1/2 * 1/2 = 1/8
, тогда 1 − 1/8 = 7/8
вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты.
а) 3/4
б) 7/8
z = (x-2)^2+2*y^2-10
1. Найдем частные производные.
На фото
2. Решим систему уравнений.
2*x-4 = 0
4*y = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 2
4*y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 2
Количество критических точек равно 1.
M1(2;0)
3. Найдем частные производные второго порядка.
На фото
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2;0)
На фото
AC - B2 = 8 > 0 и A > 0 , то в точке M1(2;0) имеется минимум z(2;0) = -10
Вывод: В точке M1(2;0) имеется минимум z(2;0) = -10;