Восточному цепочки вычислений а)48+39=87-7=804=320-120=200: 5=40 б)60: 3=20+90=110-40=704=280-200=80 7=+21=+50= : 6=8=160

👇

Увидеть ответ

Ответ:

Айка12341

21.07.2021

48+39=87-7=80*4=320-120=200
232,5-200= 32,5*4=130-40=90+90=180/3=60

4,4(90 оценок)

Открыть все ответы

Ответ:

маша3047

21.07.2021

1. в ящике 120 кг пшена. после того как из ящика отсыпали пшено в мешок, в ящике осталось 65% всего пшена. сколько кг пшена вошло в мешок?

решение: 120*0,65=78кг осталось в мешке

120-78=42 кг пшена вошло в мешок

ответ: 42 кг

2. в роще 700 берёз и 300 сосен. сколько поцентов всех деревьев составляют сосны?

решение: всего в роще 1000 деревьев

(300/1000)*100=30 % всех деревьев

ответ: 30 %

3. СО СКЛАДА ВЫГРУЗИЛИ 244,8 Т УГЛЯ, ПОСЛЕ ЧЕГО НА СКЛАДЕ ОСТАЛОСЬ 55% УГЛЯ. СКОЛКО ТОНН УГЛЯ БЫЛО НА СКЛАДЕ?

решение: 244,8 т = 45%

х = 100 %

х=(244,8*100)/45 = 544 т

ответ: 544 т

4. Товар стоил 4800 рублей.Перед праздниками его цена снизилась на 12%.Какова новая цена товара?

решение: 4800*0,88=4224 рублей

ответ: 4224 рублей

5.Решите уровнение: 1,7Х+21+3,1Х=57

решение: 4,8х=36

х=7,5

ответ: 7,5

6. В пакете лежали сливы. Сначала из него взяли 50% слив,а потом 40% остатка. После этого в пакете осталось 3 сливы.Сколько слив было в пакете первоночально?

решение: 1. 3 - 60%

х - 100%

х= 5 слив

2. 5 - 50%

х - 100%

х = 10 слив

ответ: 10 слив

4,7(96 оценок)

Ответ:

sanny2

21.07.2021

Дана функция: f(x)=x^4-6x^2+4.

Общая схема исследования и построения графика функции

1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.

Область определения функции D(x)( = R.

При определении области значений функции задача сводится к нахождению наибольшего и наименьшего значения функции (это будет в пункте 8).

2. Выяснить, является ли функция четной или нечетной.

Проверим функцию чётна или нечётна с соотношений f = f(-x) и f = -f(-x).

(-x)^4-6*(-x)^2+4 = x^4-6x^2+4.
То есть, f = f(-x). Функция чётная.

3. Выяснить, является ли функция периодической - нет.

4. Найти точки пересечения графика с осями координат (нули функции).

График функции пересекает ось X при f = 0
значит надо решить уравнение:

x^4−6x^2+4=0.
Замена: х^2 = t.
Имеем квадратное уравнение t^2-6t+4=0
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:D=(-6)^2-4*1*4=36-4*4=36-16=20;
Дискриминант больше 0, уравнение имеет 2 корня:t_1=(√20-(-6))/(2*1)=(√20+6)/2=√20/2+6/2=√20/2+3 =
= √5 + 3 ≈ 5.236068;t_2=(-√20-(-6))/(2*1)=(-√20+6)/2=-√20/2+6/2=-√20/2+3 =
= -√5 + 3 ≈ 0.763932.
Тогда получаем 4 корня:
х_1 = -(-√5 + 3),
х_2 = √(-√5 + 3),
х_3 = -√(√5 + 3),
х_4 = √(√5 + 3).Точки пересечения с осью X:

Численное решение
x1=0.874032048898,
x2=−0.874032048898x2,x3=−2.28824561127,
x4=2.28824561127.
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^4 - 6*x^2 + 4.
0^4−0+4 = 4Результат:
f(0)=4
Точка:
(0, 4)

5. Найти асимптоты графика - их нет.

6. Вычислить производную функции f'(x) и определить критические точки.

f'(x) = 4х³ - 12х = 4х(х² - 3).

Приравниваем производную нулю: 4х(х² - 3) = 0.

Получаем 3 корня (это критические точки):

х = 0, х = √3 и х = -√3.

7. Найти промежутки монотонности функции.

Исследуем знаки производной:

х = -2 -1.732 -1.5 -0.5 0 0.5 1.5 1.732 2
y'=4х³ - 12х -8 0 4.5 5.5 0 -5.5 -4.5 0 8.
Где производная положительна - там функция возрастает, где отрицательна - там функция убывает.
Возрастает на промежутках [-sqrt(3), 0] U [sqrt(3), oo).
Убывает на промежутках (-oo, -sqrt(3)] U [0, sqrt(3)]

8. Определить экстремумы функции f(x).

Где производная меняет знак с - на + там минимум функции, где меняет знак с + на - там максимум.

экстремумы в точках:

(0, 4) максимум,

(-√ 3, -5) и (√ 3, -5) минимумы.

9. Вычислить вторую производную f''(x).

Приравниваем нулю вторую производную:

f''(x) = 12х²-12 =12(х² - 1) = 0.

Имеем 2 точки перегиба функции: х = 1 и х = -1.

10. Определить направление выпуклости графика и точки перегиба.

Вогнутая на промежутках (-oo, -1] U [1, oo).
Выпуклая на промежутках [-1, 1]

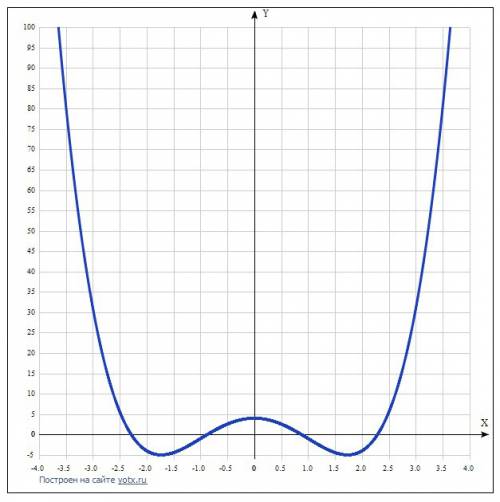
11. Построить график, используя полученные результаты исследования - в приложении.