Пошаговое объяснение:
Исследуем точку стыка промежутков в точке x₀=2
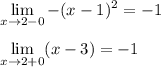
В этой точке пределы существуют и они равны, поэтому функция в этой точке непрерывна.
Исследуем точку стыка промежутков в точке x₀=3
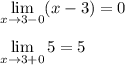
В этой точке пределы существуют, но они разные, поэтому это точка разрыва 1-го рода.
на каждом промежутке функция непрерывна.
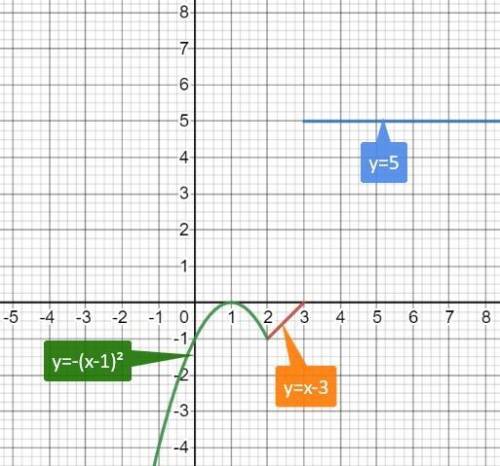
график.
a) строим -(x-1)² и ограничиваем его областью х ≤ 2
( берем известный график у=х², опускаем ветви вниз и смещаем график по оси ОХ вправо на +1)
b) строим график у=(х-3) и ограничиваем его областью 2 < x ≤ 3
(берем график у=х и смешаем его по оси ОУ на -3 вниз.)
c) ну и график у=5, ограничиваем областью х > 3
2) 300:2=150(руб)-1м ткани
3) 750:150=5(м)-во 2-м куске