Для того чтобы высчитать площадь фигуры неразрывной функции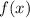 
на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
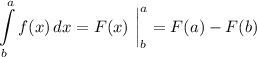
Здесь 
и 
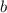— границы фигуры на оси абсцисс, 
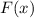— первообразная для функции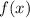
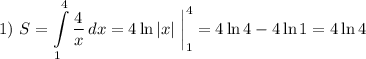квадратных единиц.
2) Здесь имеем площадь фигуры, ограниченной двумя функциям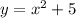и: 
и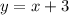 
.
Чтобы найти данную площадь, нужно найти разность площадей каждой функции.
Очевидно, что площадь фигуры, образованной функцией 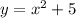на отрезке ![[-2; \ 1]](/tpl/images/1068/9083/4704b.png)
больше, чем площадь фигуры, образованной функцией 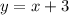на том же отрезке, поэтому
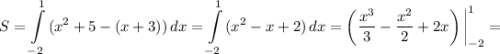
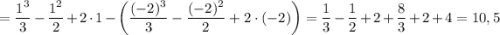квадратных единиц.
1046
a) |x|>10
1)
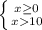2)
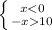
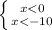
ответ: x∈(-∞;-10)∪(10;+∞)
b) |x|≤8,14
1)
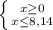2)
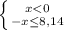
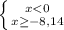
ответ: x∈[-8,14;8,14]
c) |x|< 3 5/6
1)
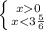2)
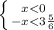
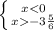
ответ: x∈(- 3 5/6;3 5/6)
d) |x|≥20
1)
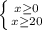2)
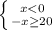
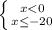
ответ: x∈(-∞;-20]∪[20;+∞)
1047
e) |x|< 16 1/9
1)
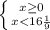2)
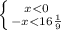
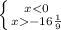
ответ: x∈(- 16 1/9;16 1/9) или -16 1/9<x<16 1/9
f) |x|< 12
1)
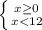2)
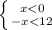
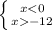
ответ: x∈(- 12;12) или -12<x<12
g) |x|< 0,8
1)
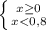2)
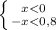
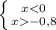
ответ: x∈(- 0,8;0,8) или -0,8<x<0,8
h) |x|≤ 2/7
1)
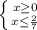2)
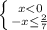
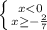
ответ: x∈[-2/7 ; 2/7] или -2/7 ≤ x ≤ 2/7
2) 40 дм = 400 см.
3) 400-24=376(см) - размер ширин прямоугольника
4) 376:2=188(см) - размер одной ширины прямоугольника.
Проверка:
Р=12+188+12+188=400 см=40 дм
ответ: ширина прямоугольника равна 188 см.