ответ. \{6\}.
Пошаговое объяснение:
Решение. Сначала найдем корни уравнения x^2-2x-4=0. Это 1\pm\sqrt{5}. Следовательно, условие x^2-2x-4\ge0 выполняется при x\le1-\sqrt{5} и при x\ge1+\sqrt{5}, а условие x^2-2x-4<0 — при 1-\sqrt{5}<1+\sqrt{5}. Рассмотрим два случая:
1) x\in\left(-\infty;1-\sqrt{5}\right]\cup\left[1+\sqrt{5};+\infty\right).
Исходное уравнение на этом множестве имеет вид x^2-2x-4=3x-2.
Его корни \displaystyle x_{1,2}=\frac{5\pm\sqrt{33}}{2}. Из них только \displaystyle\frac{5+\sqrt{33}}{2} попадает под наш случай. Докажем это:
\[\begin{array}{c} \displaystyle 1-\sqrt{5}<\frac{5-\sqrt{33}}{2}<1+\sqrt{5}\Leftrightarrow\\[2mm] \Leftrightarrow2-2\sqrt{5}<5-\sqrt{33}<2+2\sqrt{5}\Leftrightarrow\\ \Leftrightarrow-3-2\sqrt{5}<-\sqrt{33}<-3+2\sqrt{5}\Leftrightarrow\\ \Leftrightarrow3+2\sqrt{5}>\sqrt{33}>3-2\sqrt{5}. \end{array}\]
Так как \sqrt{5}>2, то 3-2\sqrt{5}<0, и, действительно, \sqrt{33}>0>3-2\sqrt{5}. Для доказательства левой части двойного неравенства возведем его в квадрат (это можно сделать, поскольку обе части неравенства неотрицательны):
P треуг = a+b+c - периметр треугольника
P треуг = 3 + 4 + 5 = 12 см
P треуг = P прямоуг = 12 см
P = 2(a+b) - периметр прямоугольника, где a, b - его стороны
12 = 2(a + b)
(a+b) = 6
S прямоуг = (a * b) = 8 см²
Решим систему:
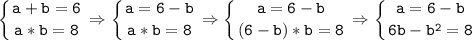
6b - b² = 8 |*(-1)
b² - 6b = -8
b² - 6b + 8 = 0
D = b² - 4ac = 36 - 4*1*8 = 36 - 32 = 4
Так как D > 0 то, квадратное уравнение имеет два действительных корня:
![\[\begin{gathered}{x_{1,2}}=\frac{{-b\pm\sqrt D}}{{2a}}=\frac{{6\pm\sqrt 4}}{{2*1}}=\frac{{6\pm 2}}{{2}}\hfill \\\\{x_1} =\frac{{6+2}}{{2}}=\frac{8}{2}=4\hfill \\\\{x_2}=\frac{{6-2}}{{2}}=\frac{{4}}{2}=2\hfill \\ \end{gathered}\]](/tpl/images/0314/5394/464ab.png)
Корнями уравнения являются: x₁ = 2, x₂ = 4, значит
b₁ = 2 см, b₂ = 4 см
a = 6 - b
a₁ = 6 - 2 = 4 см, a₂ = 6 - 4 = 2 см
ответ: 4 см, 2 см - стороны прямоугольника.
3 см 6 мм +4 см 2мм + 5 см 4 мм= 36+42+54=132мм =13 см 2 мм - периметр треугольника