111, 121, 131, 141, 151, 112, 113, 114, 115, 122, 123, 124, 125, 131, 132, 133, 134, 135, 141, 142, 143, 144, 145, 151, 152, 153, 154, 155. (в сотнях где поставлена цифра "1", также надо заменить на другие имеющиеся в самой задаче цифры)
Пошаговое объяснение:
такие задачи достаточно легкие, если следовать по порядку. сначала в решении изменяем сотни. дальше ставим в десятки любую цифру из задачи, и перебираем единицы. потом сменяем десятки, и также играем с единицами по методу 11, 12, 13, 14, 15, 21, 22, 23, 24, 25 и т. д. когда все возможные варианты с единицами и десятками перепробованы, записываем следующую сотню, и делаем все дальше как по объяснениям выше.
Задача имеет два решения.
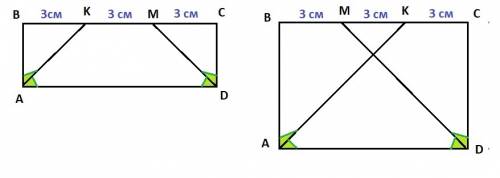
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см
AUC={-4;0;2;3;5;6;8}
B/A={-9;1;7}
B∩C={0;2}
A/C={-4;3)
(B∩C)∩(A/C)=∅
K*B={(1;-9);(2;-9);(3;-9);(1;2);(2;2);(3;2);(1;0);(2;0);(3;0);(1;1);(2;1);(3;1);(1;7);(2;7);(3;7)}